12:04 1 0,1 КБ/с.
п
57
Урок 55
Урок 55
7 клас. 14 квітня. Графік рівняння з двома змінними
Прочитайте про графік рівняння на сторінці 200 від слів "Вивчаючи якийсь
об'єкт.." до прикладу 6 на сторінці 200. ПРИКЛАД 6 переписати в зошит.
Розв'язуємо вправи.
N® 1019, 2x-y+1 = 0.
Зразок: 1) А(-3;-17). Підставимо = -3 iy=-17 в рівняння та виконаємо
обчислення. 2(-3)-(-17) + 1 = 18 + 17+ 1 = 36 +0. Отже, точка не належить
графіку рівняння.
2) В(2,9). Підставимо х = 2 і у = 9в рівняння та виконаємо обчислення.
2-21-9 +1 = 8 9 + 1 = 0. Отже, точка належить графіку рівняння.
№ 1020 Робимо те ж саме.
№ 1021. Початок координат - це точка 0(0;0).
Зразок: 1) 12х + 17y = 0. Робимо те ж саме.
Підставимо х = Oiy = 0в рівняння 12х + 17y = 0 та виконаємо обчислення:
12-0 + 17-0 = 0.Отже, графік рівняння проходить через початок координат.
№ 1024 4х + Зу = 30, A6,6).
Підставимо х = 6i y = b в рівняння. Одержимо: 4:6 +3+b = 30.
24 + 3b = 30.
Це рівняння. Розв'язуємо. 3b = 30- 24 = б.
b = 6:2 = 3.
N9 1025. Зробити самостійно.
№ 1026. Зразок: 2) x-y = 1.
Спочатку візьмемо вісь Оу. В цьому випадку х= 0. Підставимо в рівняння:
o-y=1.
Розв'язуємо: у=-1.
Відповідь: (0;-1).
Тепер візьмемо вісь Ох. В цьому випадку у = 0. Підставимо в рівняння:
x -0 = 1.
Розв'язуємо, х = 1.
Відповідь: (10).
№ 1029. Зразок: 1) А(-2,2),
Візьмемо будь-який вираз. Наприклад, 2х + 5y = ?
Щоб знати, яке число слід записати справа, Підставимо в рівняння ці числа
x = -2iy= 2. Одержимо: 2-(-2) + 5:2 = 6,
Отже, замість знака ? в правій частині слід написати б.
Відповідь: 2 + 5y = 6.
Завдання для самостійної роботи; N 1019. 1020. 1021(2), 1025. 1026(1).
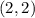
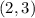
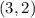
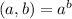- где a-число оценок, b-число учеников.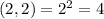
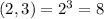
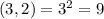
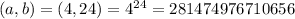
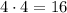- варианта событий.
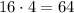- варианта событий.
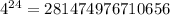- вариантов событий.
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.