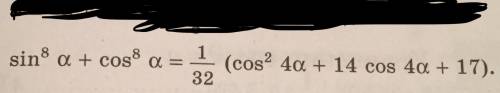
![Cos2\alpha=m\\\\Cos^{2}\alpha=\frac{1+Cos2\alpha }{2}=\frac{1+m}{2}\\\\Sin^{2}\alpha=\frac{1-Cos2\alpha }{2}=\frac{1-m}{2}\\\\Sin^{8}\alpha +Cos^{8}\alpha=(\frac{1-m}{2})^{4}+( \frac{1+m}{2})^{4} =\\\\=\frac{1}{16}[(1-m)^{4}+(1+m)^{4}]=\\\\=\frac{1}{16}(1-4m+6m^{2} -4m^{3}+m^{4}+1+4m+6m^{2}+4m^{3}+m^{4})=\\\\=\frac{1}{16}(2m^{4}+12m^{2}+2)=\frac{1}{8}(m^{4}+6m^{2}+1)=\\\\=\frac{1}{8}(Cos^{4}2\alpha+6Cos^{2}2\alpha+1)=](/tpl/images/1802/3642/e76a9.png)
![=\frac{1}{8}[(\frac{1+Cos4\alpha }{2})^{2}+6 (\frac{1+Cos4\alpha }{2})+1]=\\\\=\frac{1}{8}(\frac{1+2Cos4\alpha+Cos^{2}4\alpha}{4}+3(1+Cos4\alpha)+1)=\\\\=\frac{1}{32} (1+2Cos4\alpha+Cos^{2}4\alpha+12+12Cos4\alpha+4)=\\\\=\boxed{\frac{1}{32}(Cos^{2}4\alpha+14Cos4\alpha+17)}](/tpl/images/1802/3642/6446e.png)
«Над пропастью во ржи», также в других переводах — «Ловец на хлебном поле», «Обрыв на краю ржаного поля детства» (англ. The Catcher in the Rye — «Ловец во ржи», 1951) — роман американского писателя Джерома Сэлинджера, входит в 100 мировых книг. В ней от лица 16-летнего юноши, по имени Холден откровенно рассказывается о его обострённом восприятии американской действительности и неприятии общих канонов и морали современного общества. Произведение имело огромную популярность как среди молодёжи, так и среди взрослого населения, оказав существенное влияние на мировую культуру второй половины XX века.
Роман был переведён почти на все основные языки мира[1]. В 2005 году журнал Time включил роман в список 100 лучших англоязычных романов, написанных начиная с 1923 года, а издательство Modern Library[en] включило его в список 100 лучших англоязычных романов XX столетия. Однако, несмотря на это в США роман часто подвергался критике и запрещён в нескольких школах из-за большого количества нецензурной лексики
Объяснение:
9
Объяснение:
Чертеж во вложении.
Пусть МА и МВ - две касательные. О-центр окружности, ОА - радиус.
По свойству касательных ОА⊥МА, ОВ⊥МВ.
В силу равенства прямоугольных треугольников МОА и МОВ по гипотенузе и катету, углы АМО и ВМО также будут равны. Значит, MO- биссектриса угла АМВ и угла АОВ.
Пусть Н - точка пересечения биссектрисы МО и хорды АВ. Т.к. МА=МВ, то треугольник АМВ - равнобедренный, тогда МН-высота и медиана. Значит, АН=ВН=7,2 см.
В треугольнике АНМ по теореме Пифагора
Т.к. АН-высота прямоугольного ∆ОАМ, то АН²=OH·НМ
7,2²=ОН·9,6
ОН=51,84/9,6=5,4
В треугольнике АНО по теореме Пифагора