1)Докажите нер-во: 1. 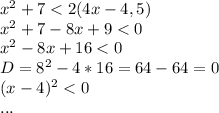
Не знаю, честно говоря что здесь требуется конкретно док-ть, прости. Т.к. тут квадрат меньше 0..
2.
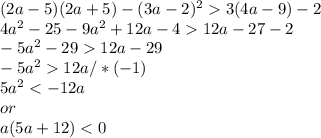
3.
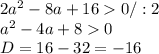
Вот тут могу док-ть и обосновать, т.к. данное квадратное ур-ие - вечный "плюс" и поэтому оно всегда будет больше 0 по определению. Вечный плюс, т.к. его дискриминант меньше 0.
2)Известно, что 7 <a <9. Оцените значение выражений:
1. a-3

2. -5a
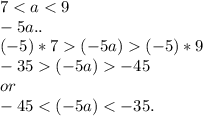
3) Дано 4 <a <3b, 2 <b <3 Оцените значение выражений: 1. а-3b
2. b-4а
3. ab
Не могу подсказать, забыла как это делать:с. Могу до утра еще исправить, если время будет. Условие я правильно записала твоих заданий?
tg α – tg β = tg (α – β) (1 + tg α tg β).
Получаем:
tg x tg 2x tg 3x = tg 3x – tg x + tg 4x – tg 2x,
tg x tg 2x tg 3x = tg 2x (1 + tg x tg 3x) + tg 2x (1 + tg 2x tg 4x),
tg 2x (1 + tg x tg 3x – tg x tg 3x + 1 + tg 2x tg 4x) = 0,
tg 2x = 0 или tg 2x tg 4x = –2.
С первым понятно, что делать. Второе:
tg 2x tg 4x = –2,
tg 2x · 2 tg 2x / (1 – tg² 2x) = –2,
tg² 2x = tg² 2x – 1.
Это равенство невозможно.
Все решения получаются из уравнения tg 2x = 0, то есть 2x = πn, x = πn/2. Значения с нечётными n не подходят (tg x и tg 3x не существуют) , значит, ответ x = πk. Возможно так