1)
Координаты точки
B(x(b), x(b-1))
C(x(c), -x(c)+3)
Так как D лежит на BC то по уравнению прямой
(6-x(b))/(x(c)-x(b)) = (4-x(b))/(4-x(b)-x(c))
(BD/CD)^2 = ((x(b)-6)^2+(x(b)-4)^2)/((x(c)-6)^2+x(c)^2) = 1/9
Решение системы
(x(b),x(c)) = (4,0) (6,6)
Значит B(4,3) и C(0,3) или B(6,5) и C(6,-3)
Так как точка D находится на стороне, а не не луче BC то подходит B(6,5) и C(6,-3)
x-1=3-x откуда x=2 y=1 и A(2,1)
Треуголник прямоугольный, значит центр описанной окружности лежит в середине гипотенузы, откуда O(6,1) R=4
(x-6)^2+(y-1)^2=16
2)
D лежит на параболе , тогда 9=2*p*6 или p=3/4
Касателтная к параболе имеет вид y*y(D) = p(x+x(D))
Откуда касательная y=(x+6)/4
F(x(d) , (x(d)+6)/4)
Так как FD=FC и D(6,3) C(6,-3)
То FC тоже касательная откуда F(-6,0)
Тогда высота от точки F то прямой DC , h=12 , S=CD*h/2 = 12*6/2 = 36
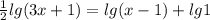
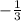, x > 1 ⇒ x > 1. 
при условии существования логарифмов. В нашем случае это тоже работает: данные логарифмы десятичные, значит, в основании 10. Вспомним, что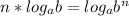 
(также при условии существования логарифма). Сразу вычислим lg1 - чтобы получить из 10 1, нужно 10 возвести в нулевую степень, значит, что 0. Тогда наше уравнение равносильно такому: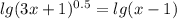 
1) 20√6 - ((16/2) + 2*(4/√2)*5√3 + 75) = 20*√2*√3 - (40√3/√2) – 83.
Приведём к общему знаменателю.
(20*√2*√3*√2 - 40√3 – 83*√2)/ √2 = (40√3 - 40√3 – 83*√2)/ √2 =
= – 83*√2/ √2 = -83.
2) У первой функции решение от х= -1 до х = 6 и х = 9.
Находим корни второй функции: х² - х - 6 = 0. Д = 1 - 4*1*(-6) = 25.
х = (1 - 5)/2 = -2, х = (1 + 5)/2 = 3.
Положительные значения функции при х меньше -2 и больше 3.
Левая часть не имеет решения, а в правой 4 корня с целыми значениями: 4, 5, 6 и в точке х = 9.
ответ: сумма равна 24.