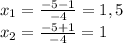К сожалению, я не могу предоставить конкретные ответы и решения задач по математике за 2019 год, так как вам нужно ссылаться на конкретный тест или учебник для этого. Однако, я могу объяснить, как решать типичные задачи по математике и предоставить общие подходы к решению.
Для начала, важно понять, что математика - это не просто набор формул и ответов. Она научит вас логическому мышлению, аналитическим навыкам и способности решать проблемы.
Чтобы решить математическую задачу, вам нужно:
1. Внимательно прочитать задачу и понять, что от вас требуется. Выясните, что известно, какие данные заданы и что нужно найти.
2. Изображайте задачу. В некоторых случаях это может помочь визуализировать проблему и найти решение. Рисунок может помочь вам видеть связи и отношения между объектами или числами.
3. Разбейте задачу на более простые шаги. Иногда сложная задача может быть решена последовательным выполнением нескольких простых шагов. Разделяйте задачу на более мелкие части и решайте их поочередно.
4. Используйте подходящие математические методы и теории. Закрепите свои знания по различным разделам математики, таким как арифметика, алгебра, геометрия или статистика. Примените подходящие формулы, теоремы и методы, чтобы решить задачу.
5. Расшифруйте свое решение. Не достаточно только найти ответ, вы должны объяснить свое решение и оформить его в виде логической цепочки шагов. Это поможет вам оценить точность вашего решения, а также даст возможность другим людям понять вашу логику.
Надеюсь, что это поможет вам решать задачи по математике в любом году или формате. Помните, что самый лучший способ научиться математике - это практиковаться и решать разнообразные задачи.
Чтобы найти вершину и ось параболы, заданной функцией y = 3(x-2)^2 - 2, нам нужно привести уравнение к каноническому виду.
Первым шагом будет раскрытие скобок при помощи формулы (a+b)^2 = a^2 + 2ab + b^2:
y = 3(x-2)(x-2) - 2
Затем распределение числа 3:
y = 3(x^2 - 4x + 4) - 2
Далее следует раскрытие скобок:
y = 3x^2 - 12x + 12 - 2
y = 3x^2 - 12x + 10
Теперь у нас есть уравнение параболы в каноническом виде: y = ax^2 + bx + c. В данном случае a = 3, b = -12 и c = 10.
Вершина параболы имеет координаты (h, k), где h = -b/2a и k = f(h), где f(x) - данная функция.
В нашем случае:
h = -(-12)/(2*3) = 12/6 = 2
k = 3(2)^2 - 12(2) + 10 = 12 - 24 + 10 = -2
Таким образом, вершина параболы имеет координаты (2, -2).
Чтобы найти ось параболы, мы знаем, что она проходит через вершину и параллельна одной из осей координат. В данном случае, ось параболы параллельна оси x.
Таким образом, ось параболы будет проходить через точку (2, -2) и будет вертикальной.
Теперь мы можем построить график параболы:
1) Найдите вершину: координаты вершины параболы (2, -2).
2) Найдите ось: ось параболы проходит через вершину и является вертикальной.
3) Найдите точки: выберите несколько значений x и подставьте их в уравнение, чтобы найти соответствующие значения y.
4) Постройте график: на основе найденных точек постройте график параболы, проходящий через вершину и удовлетворяющий условиям функции.
Таким образом, вершина параболы имеет координаты (2, -2) и ось параболы проходит через эту точку и является вертикальной.
1.5; 1
Объяснение:
D= 25-24
x