Решение системы уравнений v=12
z=15
Объяснение:
Решить систему уравнений методом подстановки.
2)(z+v)/9 - (z-v)/3 =2
(2z-v)/6 - (3z+2v)/3= -20
Избавимся от дробного выражения, первое уравнение умножим на 9, второе на 6:
(z+v) - 3(z-v)=9*2
(2z-v) - 2(3z+2v)= 6*(-20)
z+v - 3z+3v=18
2z-v - 6z-4v= -120
Приводим подобные члены:
4v-2z=18
-4z-5v= -120
Выразим z через v в первом уравнении, подставим выражение во второе уравнение и вычислим v:
-2z=18-4v
2z=4v-18/2
z=2v-9
-4z-5v= -120
-4(2v-9)-5v= -120
-8v+36-5v= -120
-13v= -120-36
-13v= -156
v= -156/-13
v=12
z=2v-9
z=2*12-9
z=15
Решение системы уравнений v=12
z=15
№1
Пусть x-скорость лодки по течению, тогда y-скорость лодки против течения. Составим систему уравнений:
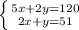
Домножим нижнее уравнение на -2
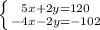
Решим методом сложения:
5x+2y-4x-2y=120-102
x=18
Подставим значение х во второе уравнение и найдем y:
2*18+y=51
36+y=51
y=51-36
y=15
Пусть скорость течения-x, а скорость лодки - y. Составим систему уравнений:
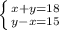
Решим методом сложения
x+y+y-x=32
2y=32
y=32/2
y=16
Подставим значение y в первое уравнение и найдем x:
x+16=18
x=18-16
x=2
ответ: скорость течения реки- 2км/ч. скорость лодки - 16 км/ч
№2
Пусть x- возраст отца, y-возраст сына
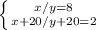
Выразим x из первого уравнения:
x/y=8
x=8y
Подставим значение x во второе уравнение:
8y+20/y+20=2
Перемножим методом креста:
2y+40=8y+20
-6y=-20
y=20/6
Выразим x:
x=8*20/6
x=80/3
Прибавим по 20 к x и y
x+20=80/3+20=140/3=46
y+20=20/6+20=140/6=23
ответ: Сыну 23 года, Отцу 46 лет.
Объяснение:
Примечания: возведение в степень - общепринятое ^a (гдн а - степень), корень это sqrt.
1) выражение под корнем должно быть неотрицательно:
след-о D(x) = (-бесконечности до 0) U (от 1 до бесконечности);
2) Тоже самое под корнем выражение должно быть неотрицательно:
под корнем модуль след-о любое выражение под корнем - положительно.
след-о D(x) = R