Задача на совместную работу. В таком случае вся выполненая раьота принимается за единицу.
Пусть х производительность 1-го рабочего, у- 2-го рабочего, тогда за 1 день первый выполнит 1\х, а второй 1\у, вместе за один день 1\12. Получим уравнение: 1\х +1\у =1\12.
х\2 – это время, которое потратит 1 на половину всей работы, а у\2 – время второго, вместе они справятся за 25 дней. Получим уравнение: х\2 + у\2 = 25. Решим эти уравнения в системе.
1\х +1\у =1\12
х\2 + у\2 = 25, решим методом подстановки, из второго уравнения х+у+ 50, х=50-у,
1\50-у + 1\у= 1\12, 12у+12(50-у)=50у-у^2 , у^2- 50у+600=100, Д=100, у=30, у=20,
Х=20, х=30. ответ: 20и 30 дней
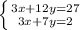
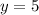, а х находим, подставив y в любое из уравнений системы. Удобнее в 1ое в данном случае. Получаем x + 4 * 5 = 9, откуда x = -11.
4 км/час и 6 км/час
Объяснение:
пусть х км/час - скорость 1- го пешехода( х>0),
у км /час-скорость 2-го пешехода у>0)
(12/х) час-время в пути первого пешехода до встречи,
(12/ у) час-время в пути 2-го пешехода до встречи
по условию задачи известно, что первый был в пути на 1 час больше(в условии сказано, что один из них вышел на один час раньше второго. я выбрала , что это первый пешеход)
уравнение:
(12/ х)-(12/у)=1
по условию известно, что если бы пешеходы вышли одновременно, то встретились бы через 2 часа 24 минуты (144/60 час), тогда (х+у) км/час - скорость сближения
уравнение:
(х+у)*(144/60)=24
система уравнений:
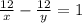
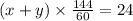
решить систему уравнений, получим х=4 км/час
у=6 км/час
Всю работу нужно принять за 1. Через две переменные ввести скорость выполнение работы (продуктивность, т.е. какую часть работы рабочий выполнит за 1 час) каждого. Тогда, если всю работу (1) мы разделим на продуктивность первого рабочего х, мы получим сколько времени понадобиться рабочему, чтобы самостоятельно выполнить всю работу. Аналогично для второго, но делить нужно на y.
И где-то несостыковка в часах/днях.
Решение прилагается.