ответ: Решение задачи, решение уравнения прикреплю в фото.
Объяснение руб.) - стоит 4 альбома и 2 ластика (2 альб.*2+1 ласт.*2)
2) 86-66=20 (руб.) - стоит альбом (4 альб. + 2 ласт. - 3 альб.-2 ласт.)
3) 20*2=40 (руб.) - стоят два альбома.
4) 43-40=3 (руб.) - стоит один ластик.
ОТВЕТ: стоимость альбома 20 рублей, стоимость ластика 3 рубля Пусть х рублей - цена альбома, а ластик стоит у рублей.
Тогда, 3х+2у=66 (первое уравнение)
2х+у=43 (второе уравнение).
Составим и решим систему уравнение (методом сложения):
2x+2y=66
2x+y=43
(умножим второе уравнение на -2)
3x+2y=66
-4x-2y=86
=(3х+(-4х)) + (2у+(-2у))=66+(-86)
-х=-20
х=20 (руб.) - стоимость альбома.
2х+у=43
2*20+у=43
у=43-40
у=3 (руб.) - стоимость ластика.
ОТВЕТ: стоимость альбома 20 рублей, стоимость ластика 3 рубля.
![\displaystyle p(x)= \left \{ {{ \dfrac{1}{b-a},~~~ x\in [a;b] } \atop {0~~~ ~~~,~~x\notin [a;b]}} \right.](/tpl/images/0836/3813/a72ca.png)
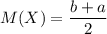
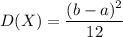
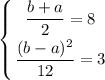получим: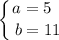 
![p(x)=\displaystyle \left \{ {{ \frac{1}{6},~~~ x\in[5;11] } \atop {0,~~~ x\notin[5;11]}} \right.](/tpl/images/0836/3813/eadb5.png)
Объяснение:
1)б
2)а
3)в
4)г
..... ....................