Задание 1
Попробуем каждую из пар чисел. Какая даст верное тождество, та и есть решение.
а)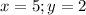 
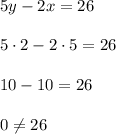
Этот вариант не подходит. Проверяем дальше.
б)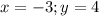 
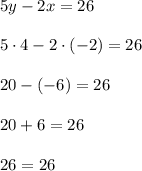
Этот вариант подходит. Проверяем дальше.
в)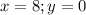 
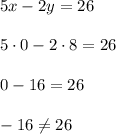
Этот вариант не подходит. Проверяем последнюю пару чисел.
г)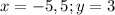 
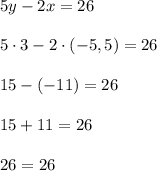
Этот вариант подходит.
ответ к Заданию 1: Решениями уравнения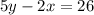 
являются пары чисел 
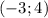и 
.
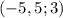Задание 2
Пара чисел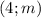 
является решением уравнения . Нужно найти . Второе число это координата 
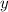. Это означает, что 
.
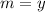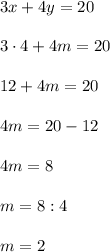
ответ к Заданию 2: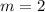 
Задание 3
При каком значении 
пара чисел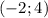 
будет являть решением уравнения?
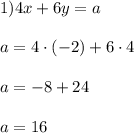
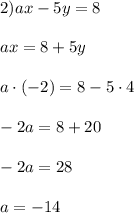
ответ к Заданию 3: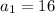 
; 
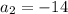
Задание 4
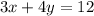
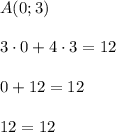
Точка А принадлежит графику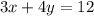 
.
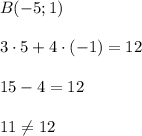
Точка B не принадлежит графику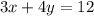
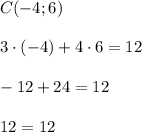
Точка C принадлежит графику .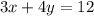
ответ к Заданию 4: точки А и С принадлежат графику 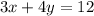, а точка В не принадлежит этому графику.
2sinxcosx-√3cosx=0
cosx(2sinx-√3)=0
cosx=0⇒x=π/2+πn,n∈Z
sinx=√3/2⇒x=(-1)^n*π/3+πk,k∈Z
б)sin 2x=√2 cos x
2sinxcosx-√2cosx=0
cosx(2sinx-√2)=0
cosx=0⇒x=π/2+πn,n∈Z
sinx=√2/2⇒x=(-1)^n*π/4+πk,k∈Z в)sin(0,5п+x)+ sin 2x=0
г)cos(0,5п+x)+ sin 2x=0
-sinx+2sinxcosx=0
-sinx(1-2cosx)=0
sinx=0⇒x=πn,n∈Z
cosx=1/2⇒x=+-π/3+2πk,k∈Z
д)sin 4x+√3 sin 3x+sin 2x=0
2sin3xcosx+√3sin3x=0
sin3x(2cosx+√3)=0
sin3x=0⇒3x=πn,n∈Z⇒x=πn/3,n∈Z
cosx=-√3/2⇒x=+-5π/6+2πk,k∈Z
е)cos 3x+sin 5x=sin x
cos3x+sin5x-sinx=0
cos3x+2sin2xcos3x=0
cos3x(1+2sin2x)=0
cos3x=0⇒3x=π/2+πn,n∈Z⇒x=π/6+πn/3,n∈Z
sin2x=-1/2⇒2x=(-1)^(k+1)*π/6+πk,k∈Z⇒x=(-1)^(n+1)*π/12+πk/2,k∈Z