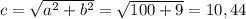
x^2+y^2=29 умножим на 4
получим 4x^2+4y^2=116 =>
y^2-4x^2=9
+
4x^2+4y^2=116
y^2+4y^2+4x^2-4x^2=9+116
сократим ( 4x^2 - 4x^2 ) => y^2+4y^2=125
5 y^2=125 поделим на пять
y^2= 25
y=+- 5
если y= -5, то (-5)^2 - 4x^2 = 9
25 - 4x^2=9
-4x^2 = 9-25
-4x^2= - 16 умножим на минус один
4x^2=16 делим на четыре
x^2=4
x= +-2
если y= 5, то 5^2 - 4x^2 = 9
25 - 4x^2=9
-4x^2 = 9-25
-4x^2= - 16 умножим на минус один
4x^2=16 делим на четыре
x^2=4
x= +-2
ответ: 1) x=2, y=5
2) x= -2, y=5
3)x= -2, y= -5
4) x=2, x= -2, y= -5
Решение системы уравнений х₁=1 х₂=3
у₁=1 у₂=7
Объяснение:
Решить систему уравнений:
ху-2у-4х= -5
у-3х= -2
Выразим у через х во втором уравнении, подставим выражение в первое уравнение и вычислим х:
у= -2+3х
х(-2+3х)-2(-2+3х)-4х= -5
-2х+3х²+4-6х-4х= -5
Приведём подобные члены:
3х²-12х+9=0, квадратное уравнение, ищем корни:
х₁,₂=(12±√144-108)/6
х₁,₂=(12±√36)/6
х₁,₂=(12±6)/6
х₁=6/6
х₁=1
х₂=18/6
х₂=3
у= -2+3х
у₁= -2+3*1
у₁=1
у₂= -2+3*3
у₂=7
Решение системы уравнений х₁=1 х₂=3
у₁=1 у₂=7