Для этого надо построить графики функций, из которых состоит система, в одной системе координат, точки пересечения этих графиков будут решениями системы. 1) график - прямая линия, для построения нужны 2 точки. x=0; y=6,5; (0;6,5) y=0; x=2,6 (2,6;0) строим график(см. вложение, красным цветом) 2) график - прямая линия, для построения нужны 2 точки. x=0; y=-3; (0;-3) y=0; x=1,5; (1,5;0) строим график(см. вложение,синим цветом) как видно из графика, прямые пересекаются в одной точке => данная система имеет только одно решение
Для начала найдем ОДЗ:
Первое уравнение решим отдельно.
3x^2 -2>0
3x^2 -2=0
x^2=2/3
Чертим координатную прямую, отмечаем точки, расставляем знаки. Рисунок добавлю во влажения.
Решением этого уравнения будет промежуток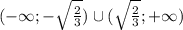
А решением системы будет являться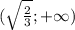
Теперь начнем решение. Представим 4 в виде логорифма по основанию x.
Так как основания равны, то знак логорифма можно опустить.
3x^2 -2 =x^4
x^4 - 3x^2 +2 =0
Это биквадратное уравнение. Введем обозначения
x^2 = a,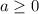
a^2 -3a+2=0
По теореме Виета a1=2, a2=1
Теперь найдем х:
x^2= 2 x^2=1
Выберем корни, входящие в ОДЗ. Таковыми являются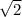 и 1.
и 1.
ответ: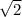 и 1
и 1