ответ: 1 -------------------------------------- если коэффициенты действительно такие, то это уравнение решается лишь за формулами Кардано (на подобие формул корней квадратного уравнения, только для уравнения 4-го степени). И тут не применишь и метод неопределенных коэффициентов (ax^2+bx+c)(dx^2+ex+f)=5x^4-12x^3+11x^2-12x+5, так как коэффициенты b,c,e,f - иррациональны. Формулы Кардано в обычном курсе алгебры в школе не изучают, в углубленном курсе кажется так же не изучают. Прикрепляю скрин
, , , , ,
два случая: 1)
2)
ответ: 1 и 5 ------------------------------ - парабола ветками вверх, нам нужен случай, когда вершина параболы лежит на оси ОХ, т.е. когда парабола пересекает эту ось в одной точке. И это будет тогда и только тогда, когда дискриминант обращается в нуль: Получили, что это случается если
См объяснение
Объяснение:
а) так как перед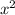 стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх
стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх
б) координаты вершины (x0, y0) вычисляются по формуле:
x0 =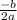 =
= 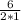 = 3
= 3
y0 = y(x0) = 9 - 6*3 +5 = -4
Значит, координаты вершины : (3, -4)
c) Ось симметрии задается уравнением: x = 3
d) По теореме Виета:
Если x1, x2 - корни квадратного уравнения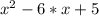 , ТО
, ТО
Отсюда получаем корни x1 = 1; x2 = 5
Эти корни и есть нули функции
e) Дополнительные точки можно найти путем подстановки любых чисел: например, пусть x=0. тогда y = y(0) = 5
f) см прикрепленный рисунок