144 км.
Объяснение:
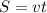
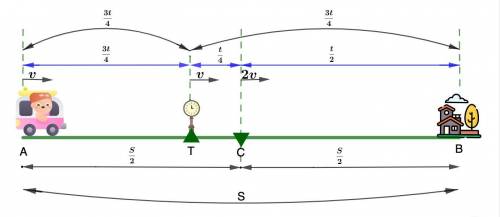
Пусть С - середина пути.
Скорость первой половины пути =  км/ч, тогда скорость второй половины -
км/ч, тогда скорость второй половины - 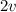 км/ч
км/ч
Пусть t ч - время первой половины пути, то есть АС.
Значит
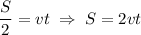 (км) (1)
(км) (1)
Так как АС = СВ, а скорость на СВ в два раза больше, чем на АС, то следует, что время на СВ в 2 раза меньше, то есть 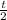 ч.
ч.
Итого время в пути
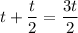 (ч), а половина времени
(ч), а половина времени 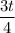 ч.
ч.
Видим, что половина времени меньше t ч, значит эта точка будет находиться на АС, предположим это точка Т.
Найдем время, за которое Тоша проедет участок ТС:
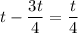 ( ч)
( ч)
Известно, что ТВ - АТ = 36 км
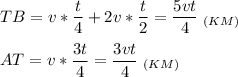
Составим уравнение:
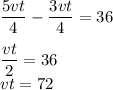
Найдем расстояние (1):
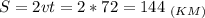
1) y =x^3+x-6
y=x^3 Находим производную по формуле степенной функции
x∧n = n*x∧(n-1)
получаем: 3х∧2
производная от х равна 1
Производная от 6 как от постоянной равна 0
Получаем производную от данной функции:
3х∧2 + 1
2) y= -1/x^3+1/x+1
Вначале преобразуем нашу функцию:
у = - х∧(- 3) + х∧(- 1) + 1
Находим производную от ( - х∧(- 3)) по формуле степенной функции
x∧n = n*x∧(n-1)
получаем: -3х∧(-3+1) =-3х∧(-4) = - 3/х∧4
Находим производную от(х∧(- 1)) по формуле степенной функции
x∧n = n*x∧(n-1)
получаем: - х∧(-2) = -1/√х
Производная от1 как от постоянной равна 0
Получаем производную от данной функции:
- 3/х∧4 + -1/√х