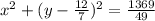1.Диагонали в прямоугольнике равны (AC=BD) и точкой пересечения O делятся пополам, то есть, BD=2BO, следовательно,
AC=2BO=2∙8=16.
ответ: 16.
2.Ритмическое движение неровное, что придает взволнованности и напряженности. Не случаен и выбор тональности. Томный до-диез минор создает особую колористическую атмосферу. Несмотря на сравнительно миниатюрные размеры произведение производит неизгладимое впечатление. Глубочайшая тоска и всепоглощающая лирика отличают и выделяют прелюдию из цикла «Пьесы-фантазии». Сочинение стало популярным достаточно быстро. Сегодня оно входит в число часто исполняемых композиций среди известных пианистов по всему миру.
Пусть точка C(0, m) - центр окружности (так как по условию центр лежит на оси OY, то первая координата равна 0)
Известно, что расстояние от центра до любой точки на окружности является константой и равно радиусу R окружности
Наша окружность проходит через точку 7 на оси OY, значит R = 7 - m
Также окружность проходит через точку 5 на оси OX, значит по теореме Пифагора
Приравняем это и получим уравнение:
Возвёдём в квадрат и решим уравнение:
Координата центра окружности -
Радиус окружности:
Уравнение окружности выглядит следующим:
Подставим наши числа:
ответ: