
9x2 + 3x; б) 6xy +3x2y – 12xy2
2°. Разложите на множители:
а) y(у – 1) + 2(y – 1); б) x2 – 64.
3°. Сократите дробь (x^2+ 3x)/(3a+ax).
4°. У выражение (а – b)2 – (а – b)(а + b).
5°. Решите уравнение x2 + 7x = 0.
6 У выражение: с(с – 2)(с + 2) – (с – 1)(с2 + с + 1).
7 Найдите корни уравнения 3x3 – 27x = 0.
8 Разложите на множители многочлен 2х + 2у – х2 – 2ху – у2.
2 вариант.
1°. Вынесите общий множитель за скобки:
а) 2ab – ab2; б) 5a4 – 10a3 + 10a2
2°. Разложите на множители:
а) ax – ay + 2x – 2y; б) 9a2 – 16b2.
3°. Сократите дробь (2a+4)/(a^(2 )- 4).
4°. У выражение (x – 1) (x + 1) – x(x – 3).
5°. Решите уравнение x2 – 25 = 0.
6 У выражение: (х + 1)(х2 + х + 1)
Объяснение:
Объяснение:
йоу,чувак
Мы можем сложить эти два уравнения и получить вместо закорючек:косинусов и синусов - единицу.
Ведь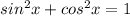
Т.е при сложении этих уравнений мы получим третье уравнение(да,мы просто сложим друг с другом почленно эти выражения, левая сторона с левой и правая сторона с правой).
Упс... чуть не забыл ОДЗ! Ведь нельзя забывать,что под корнем у нас могут находиться лишь неотрицательные числа(АУФ),но это пока мы не добрались до комплексного пространства,ну да ладно,оно сейчас не нужно. Итак составим неравенство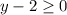
т.е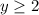 . Так-с... ОДЗ мы нашли. Вернёмся к истокам.
. Так-с... ОДЗ мы нашли. Вернёмся к истокам.
уравнение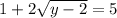 с одной переменной решается легко,всего-лишь щелчк... возведением в квадрат обеих частей уравнения!
с одной переменной решается легко,всего-лишь щелчк... возведением в квадрат обеих частей уравнения!
Мы нашли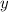 . И чему он равен? Правильно
. И чему он равен? Правильно 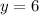
теперь подставим данное значение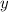 в эти уравнения.
в эти уравнения.
И получим следующее
И всё!! Задача почти решена!
Предлагаю тебе обратиться к таблице синусов и косинусов и посмотреть, при каких значениях синус обращается в нуль,а косинус в 1.
синус обращается в нуль,а косинус в 1.
Удачи тебе, my dear!