решаем по свойству пропорции
x-4=2(x+4)
x-4=2x+8
x-2x=8+4
-x=12
x=-12


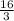
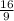
 или х₂ = 1
или х₂ = 1
Решение
Известно, что против большего угла находится большая сторона.
На вкладыше рисунок для доказательства.
Рассчитываем углы треугольника АВС: ∠ABC=∠ACB= (180-20)/2=80°
На боковой стороне AC треугольника ABC отложим отрезок CD, который равен основанию BC.
BC=CD
Треугольник BCD равнобедренный.
Рассчитываем углы в Δ BCD ∠DBC = ∠BDC = (180-80)/2 = 50°
В треугольнике ABD ∠ABD = 80 - 50 = 30°
Значит в треугольнике ABD ∠ABD больше, чем ∠BAD (30° больше 20°), поэтому AD больше, чем BD больше, чем BC
(в равнобедренном треугольнике BDC основание
BD лежит против большего угла C).
Вывод: AC = AD + CD > BC + CD = 2BC.
Рисунок во вкладыше
х-4 / х + 4 = 2
х-4 / х = 2 - 4
х-4 / х = -2
-2х = х-4
-2х-х= -4
-3х= -4
х = 4/3
х = 1 1/3