Решить уравнения за 7класс 0,15(x-4)=9,9-0,3*(x-1) (0,7x-2,,5-2x)=0,9(3x-1)+0,1

👇

Ответ:

rita1501

11.02.2023

А)0,15(x-4)=9,9-0,3*(x-1)
0,15x-0.6=9.9-0.3х+0.3
0,15x+0.3х=0.6+0.3+9.9
0.18х=10.8
х=60
Б)(0,7x-2,1)-(0,5-2x)=0,9(3x-1)+0,1
0,7x-2,1-0,5+2x=2.7х-0.9+0.1
0,7x-0,7x+2x=2,1+0,5-0.9+0.1
2х=1.8
х=0.9

4,7(48 оценок)

Открыть все ответы

Ответ:

gree04

11.02.2023

Решение:

Немного теории. Систему уравнений можно записать в следующем виде:

A·x = b

где A - матрица коэффициентов, x - вектор-столбец переменных, b - вектор-столбец свободных членов.

Умножим эту систему на обратную матрицу коэффициентов A⁻¹ слева. Тогда:

A⁻¹·A·x = A⁻¹·b

x = A⁻¹·b

Таким образом, чтобы решить систему уравнений, нужно найти обратную матрицу коэффициентов и умножить ее на вектор-столбец свободных членов.

1) Обратная матрица

Будем искать обратную матрицу через алгебраические дополнения. Для начала найдем определитель матрицы A :

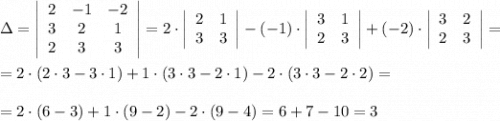
$\Delta =\left|\begin{array}{ccc}2&-1&-2\\3&2&1\\2&3&3\end{array}\right|=2\cdot \left|\begin{array}{cc}2&1\\3&3\end{array}\right|-(-1)\cdot \left|\begin{array}{cc}3&1\\2&3\end{array}\right|+(-2)\cdot \left|\begin{array}{cc}3&2\\2&3\end{array}\right|=\\\\=2\cdot(2\cdot3-3\cdot1)+1\cdot(3\cdot3-2\cdot1)-2\cdot(3\cdot3-2\cdot2)=\\\\=2\cdot(6-3)+1\cdot(9-2)-2\cdot(9-4)=6+7-10=3$

Найдем элементы матрицы алгебраических дополнений:

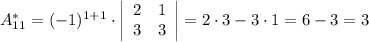
$A_{11}^{*}=(-1)^{1+1}\cdot \left|\begin{array}{cc}2&1\\3&3\\\end{array}\right|=2\cdot3-3\cdot1=6-3=3$

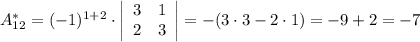
$A_{12}^{*}=(-1)^{1+2}\cdot \left|\begin{array}{cc}3&1\\2&3\\\end{array}\right|=-(3\cdot3-2\cdot1)=-9+2=-7$

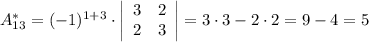
$A_{13}^{*}=(-1)^{1+3}\cdot \left|\begin{array}{cc}3&2\\2&3\\\end{array}\right|=3\cdot3-2\cdot2=9-4=5$

$A_{21}^{*}=(-1)^{2+1}\cdot \left|\begin{array}{cc}-1&-2\\3&3\\\end{array}\right|=-((-1)\cdot3-3\cdot(-2))=3-6=-3$

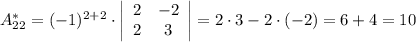
$A_{22}^{*}=(-1)^{2+2}\cdot \left|\begin{array}{cc}2&-2\\2&3\\\end{array}\right|=2\cdot3-2\cdot(-2)=6+4=10$

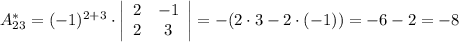
$A_{23}^{*}=(-1)^{2+3}\cdot \left|\begin{array}{cc}2&-1\\2&3\\\end{array}\right|=-(2\cdot3-2\cdot(-1))=-6-2=-8$

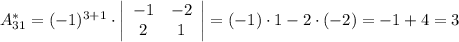
$A_{31}^{*}=(-1)^{3+1}\cdot \left|\begin{array}{cc}-1&-2\\2&1\\\end{array}\right|=(-1)\cdot1-2\cdot(-2)=-1+4=3$

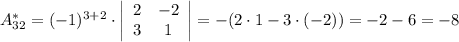
$A_{32}^{*}=(-1)^{3+2}\cdot \left|\begin{array}{cc}2&-2\\3&1\\\end{array}\right|=-(2\cdot1-3\cdot(-2))=-2-6=-8$

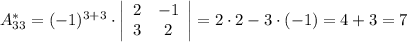
$A_{33}^{*}=(-1)^{3+3}\cdot \left|\begin{array}{cc}2&-1\\3&2\\\end{array}\right|=2\cdot2-3\cdot(-1)=4+3=7$

Тогда:

$A^*=\left(\begin{array}{ccc}3&-7&5\\-3&10&-8\\3&-8&7\end{array}\right)$

Транспонированная матрица алгебраических дополнений:

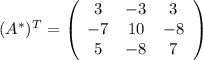
$(A^*)^T=\left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

Обратная матрица:

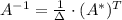
$A^{-1}=\frac{1}{\Delta} \cdot (A^*)^T$

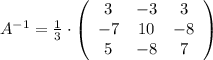
$A^{-1}=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

2) Вектор-столбец переменных

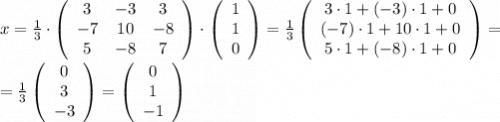
$x=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)\cdot\left(\begin{array}{ccc}1\\1\\0\end{array}\right)=\frac{1}{3} \left(\begin{array}{ccc}3\cdot1+(-3)\cdot1+0\\(-7)\cdot1+10\cdot1+0\\5\cdot1+(-8)\cdot1+0\end{array}\right)=\\\\=\frac{1}{3} \left(\begin{array}{ccc}0\\3\\-3\end{array}\right)=\left(\begin{array}{ccc}0\\1\\-1\end{array}\right)$

ответ:

x₁ = 0;

x₂ = 1;

x₃ = -1.

4,7(76 оценок)

Ответ:

karinakarim

11.02.2023

0.96, 2.88, 5.76 тонн соответственно

Объяснение:

20% это 1/5 от 12 тонн. разделим 12 на 5 = 2.4 тонны отдали в школьную столовую (если будет другой процент то надо: общее количество разделить на 100 и умножить на проценты. В данном случае 12 / 100 = 0.12 0.12 * 20% = 2.4 увезли в шк.столовку. Осталось 9.6 тонн это 12 - 2.4 = 9.6. Их развезли в магазины 1:3:6 сколько частей? 1 + 3 + 6 = 10. Оставшийся картофель зазделим на сумму всех частей = 0,96 тонны. Теперь, развезём в магазины: одну часть в первый это будет 0.96 тонны, три части 0.96 * 3 = 2.88 тонны во втрой и шесть частей 0.96 * 6 = 5.76 в третий магазин. Можно проверить:

0.96 + 2.88 + 5.76 = 9.6 тонн

9.6 + 2.4 = 12 тонн

4,4(55 оценок)

Это интересно:

Компьютеры-и-электроника

19.12.2022

Как отключить автозагрузку приложений на Android...

Питомцы-и-животные

17.04.2023

Объемная кровать для собаки: сделай сам и порадуй своего питомца...

27.02.2021

Как изменить всю свою личность: советы от психологов...