AB диаметр окружности с центром О. Найдите координаты центра окружности если A(8;7)и В (6;-1) b) Запишите уравнение окружности используя условия пункта а)
СОР РЕШИТЕ

Question

Алгебра: AB диаметр окружности с центром О. Найдите координаты центра окружности если A(8;7)и В (6;-1) b) Запишите уравнение окружности используя условия пункта а) СОР РЕШИТЕ ​

25durak · Accepted Answer

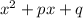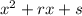Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через x^2+px+q , другой - через x^2+rx+s .

Задача сводится к нахождению p, q, r, s. Тогда

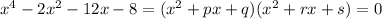
x^4-2x^2-12x-8=(x^2+px+q)(x^2+rx+s)=0

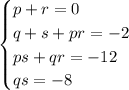
$\begin{cases} p+r=0\\q+s+pr=-2\\ps+qr=-12\\qs=-8 \end{cases}$

Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:

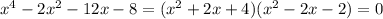
x^4-2x^2-12x-8=(x^2+2x+4)(x^2-2x-2)=0

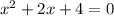x^2+2x+4=0 не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).

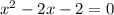
x^2-2x-2=0

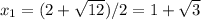
$x_1=(2+\sqrt{12})/2=1+\sqrt{3}$

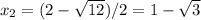
$x_2=(2-\sqrt{12})/2=1-\sqrt{3}$

Сумма корней: 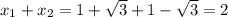$x_1+x_2=1+\sqrt{3}+1-\sqrt{3}=2$

если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:

x^4-2x^2-12x-8=(x^2-2x-4)(x^2+2x+2)=0

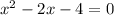
x^2-2x-4=0

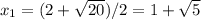
$x_1=(2+\sqrt{20})/2=1+\sqrt{5}$

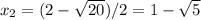
$x_2=(2-\sqrt{20})/2=1-\sqrt{5}$

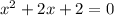x^2+2x+2=0 не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).

Сумма корней: 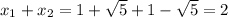$x_1+x_2=1+\sqrt{5}+1-\sqrt{5}=2$

ответ: 2.

AB диаметр окружности с центром О. Найдите координаты центра окружности если A(8;7)и В (6;-1) b) Запишите уравнение окружности используя условия пункта а) СОР РЕШИТЕ ​

MOGZ ответил

AB диаметр окружности с центром О. Найдите координаты центра окружности если A(8;7)и В (6;-1) b) Запишите уравнение окружности используя условия пункта а)
СОР РЕШИТЕ