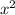-4x+1 определите ее увеличение f(x), если 
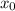= 4 и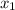 
= 2. Показать все расчеты!
Складываем оба уравнения, получим:
x² - 2 * x * y + y² = 1.
Разложим по формуле квадрата разности, получим:
(x - y)² = 1,
x - y = 1,
x - y = -1.
Вычитаем из первого системного уравнения второе, получим:
x² - y² = 3.
Разложим как разность квадратов, получим:
(x - y) * (x + y) = 3.
Следовательно, получим две системы уравнений:
1. (x - y) * (x + y) = 3 и x - y = 1,
x + y = 3 и x - y = 1.
Складываем почленно:
2 * x = 4, откуда х = 2,
y = x - 1 = 2 - 1 = 1.
2. (x - y) * (x + y) = 3 и x - y = -1,
x + y = -3 и x - y = -1,
2 * x = -4,
x = -2,
y = x + 1 = -2 + 1 = -1.
ответ: (2; 1) и (-2; -1).
(x + 2)⁴ - 5(x + 2)² + 4 = 0
замена : (х+2)² = t
t² - 5t + 4 = 0
D = (-5)² - 4*1*4 = 25 - 16 = 9 = 3²
D> 0 - два корня уравнения
t₁= (- (-5) - 3)/(2*1) = (5-3)/2 = 2/2= 1
t₂= (-(-5) + 3)/(2*1) = (5+3)/2 = 8/2= 4
(x + 2)² = 1
x² + 2*x*2 + 2² = 1
x² + 4x + 4 - 1 =0
x² + 4x + 3 = 0
D = 4² -4*1*3 = 16 - 12 = 4 = 2²
D>0 - два корня уравнения
х₁ = (-4 - 2)/(2*1) = -6/2 = - 3
х₂ = (-4+2)/(2*1) = -2/2 = - 1
(х + 2)² = 4
х² + 4х + 4 - 4 =0
х² + 4х = 0
х(х + 4) = 0
произведение = 0, если один из множителей = 0
х₁ = 0
х + 4 =0
х₂ = -4
ответ : х₁= - 4 ; х₂ = - 3 ; х₃ = - 1 ; х₄ = 0.
Объяснение:
Дай лутший