
1. Цветных шаров в ящике 5, поэтому вероятность вытащить цветной шар равна  , что равно 0,5.
, что равно 0,5.
ответ: вероятность того, что вынутый наугад шар цветной равна 0,5.
2. Еще раз напишу условие, для удобста: cos 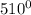 - sin
- sin 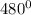 + tg
+ tg 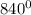 .
.
Рассмотрим каждое слагаемое в отдельности:
cos 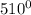 = cos
= cos 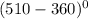 = cos
= cos 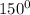 = -
= - 
sin 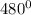 = sin
= sin 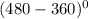 = sin
= sin 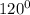 =
= 
tg 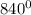 = tg
= tg 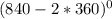 = tg
= tg 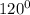 = -
= - 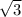
Теперь заменим слагаемые в исходном выражении полученными значениями:
cos 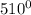 - sin
- sin 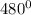 + tg
+ tg 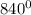 = -
= -  -
-  -
- 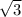 = -2*
= -2*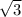
ответ: -2*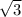
3. В физике уравнение движения точки выглядит следующим образом:
S = 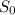 +
+ 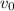 t +
t + 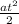
Обратимся теперь к уравнению, данному в условии:
S(t) = 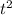 - 8t + 4
- 8t + 4
Заметим, что 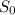 = 4,
= 4, 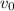 = -8, a = 2.
= -8, a = 2.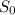
Уравнение изменения скорости:
v = 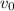 + at
+ at
Подставим в него вместо v - 0, как требуется в условии и вместо 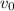 и a найденные нами значения и решим полученное уравнение:
и a найденные нами значения и решим полученное уравнение:
0 = -8 + 2t
8 = 2t
t = 4
ответ: скорость точки окажется равной нулю через 4 единицы времени после начала движения.
4. Формула объема правильного тетраэдра:
V = 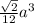 , где a - длина ребра.
, где a - длина ребра.
Пусть ребро данного тетраэдра равно l. Тогда его объем выражается формулой 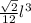 , обозначим его как
, обозначим его как 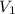 .
.
Ребро же нового тетраэдра равно 4l.
Подставим его в формулу объема, вместо a:
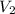 =
= 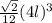 =
= 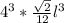 =
=  = 64
= 64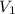
Подставим вместо 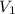 значение, данное в условии:
значение, данное в условии:
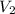 = 64*3 = 192 см
= 64*3 = 192 см
ответ: объем такого правильного тетраэдра равен 192 см
Система линейных уравнений с двумя неизвестными
x + y = 5
2x - 3y = 1
Система линейных ур-ний с тремя неизвестными
2*x = 2
5*y = 10
x + y + z = 3
Система дробно-рациональных уравнений
x + y = 3
1/x + 1/y = 2/5
Система четырёх уравнений
x1 + 2x2 + 3x3 - 2x4 = 1
2x1 - x2 - 2x3 - 3x4 = 2
3x1 + 2x2 - x3 + 2x4 = -5
2x1 - 3x2 + 2x3 + x4 = 11
Система линейных уравнений с четырьмя неизвестными
2x + 4y + 6z + 8v = 100
3x + 5y + 7z + 9v = 116
3x - 5y + 7z - 9v = -40
-2x + 4y - 6z + 8v = 36
Система трёх нелинейных ур-ний, содержащая квадрат и дробь
2/x = 11
x - 3*z^2 = 0
2/7*x + y - z = -3
Система двух ур-ний, содержащая куб (3-ю степень)
x = y^3
x*y = -5
Система ур-ний c квадратным корнем
x + y - sqrt(x*y) = 5
2*x*y = 3
Система тригонометрических ур-ний
x + y = 5*pi/2
sin(x) + cos(2y) = -1
Система показательных и логарифмических уравнений
y - log(x)/log(3) = 1
x^y = 3^12
Объяснение: