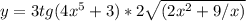
Можно эту задачу решить по формуле из физики (суть точно такая же как Вы и написали в условии). Формула такова: H=(gt(^2))/2 , то есть в числителе у нас "ж умножить на т в квадрате", а в знаменателе 2, где g-есть ускорение свободного падения(9,8 м/с(^2)), а t-это время, которое нам и нужно найти. Таким образом, из формулы выражаем величину t=sqrt(2H/g), где sqrt-корень, то есть величина 2Н/g находится под корнем. Считаем: t=sqrt(2*4410м/9,8м/с^2)=30секунд. Если вам нужно написать решение в тетрадь, то необязательно так всё расписывать, я писал так, чтобы вам было максимально понятно. В тетради же решение выглядеть должно так: H=(gt(^2))/2 сл-но t=sqrt(2H/g)=sqrt(2*4410м/9,8м/с^2)=30секунд.
Что бы построить график данной функции, исследуем данную функцию:
1. Область определения:
Так как данная функция имеет смысл при любом х. То:
2. Область значения:
Так как данная функция - квадратичная, а так же, главный коэффициент а положителен.То, график данной функции - парабола и ее ветви направлены вверх.
Следовательно, область значения данной квадратичной функции находится следующим образом (при а>0):
Найдем дискриминант:
Теперь находим саму область:
3. Нули функции:
Всё что требуется , это решить уравнение.
Следовательно, функция равна нулю в следующих точках:
4. Зная нули функции, найдем промежутки положительных и отрицательных значений.
Чертим координатную прямую, на ней отмечаем корни уравнения, записываем 3 получившийся промежутка и находим на данных промежутках знак функции:
То есть:
5. Промежутки возрастания и убывания.
Для этого найдем вершину параболы:
Промежуток убывания:
Промежуток возрастания:
Если вы изучали понятие экстремума, то:
---------------------------------------------------------------
6. Экстремум функции.
Так как а>0 и функция квадратичная. То вершина является минимумом данной функции.
Следовательно:
---------------------------------------------------------------
7. Ось симметрии
Зная вершину, имеем следующее уравнение оси симметрии:
Основываясь на данных, строим график данной функции. (во вложении).