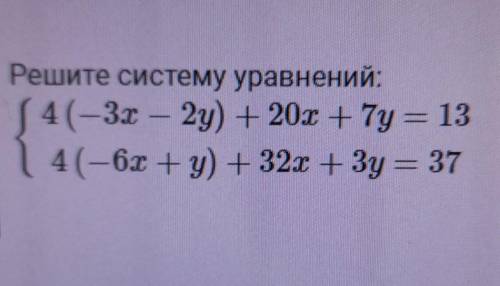
Точку пересечения мы можем найти, приравняв значения функции.
1. Для этого преобразуем первую функцию:
7х+2у=82
2у=82-7х
у=(82-7х)/2
2. Приравняем значения функции:
(82-7х)/2=-2,5х
По методу пропорции:
-5х=82-7х
7х-5х=82
2х=82
х = 41.
3. Для нахождения ординаты (у) , подставим значение аргумента (х) в любую функцию. На мой взгляд, проще использовать вторую функцию.
у= -2,5х, где х=41.
у= -2,5 * 41 = - 102,5.
4. В качестве проверки подставим значение аргумента в первую функцию. Для этого заиспользуем ранее выведенную формулу: у=(82-7х)/2.
у=(82-7х)/2, где х = 41.
у = (82 - 7*41) /2 = -205/2 = -102,5.
Ординаты сошлись => точка пересечения найдена верно.
5. Запишем ввиде координаты: ( 41; - 102,5)
ответ: ( 41; -102,5)
Объяснение:
Функция задана формулой y = -2x + 7.
Определите:
1) значение функции, если значение аргумента равно 6;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=6
у= -2*6+7= -5 при х=6 у= -5
2) значение аргумента, при котором значение функции равно -9;
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
-9= -2х+7
2х=7+9
2х=16
х=8 у= -9 при х=8
3) проходит ли график функции через точку А(-4;15).
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
15= -2*(-4)+7
15=15, проходит.
Объяснение:
4( - 3х - 2у) + 20х + 7у = 13
4( - 6 + у) + 32х + 3у = 37
8х - у = 13 l × (-4)
32х + 7у = 61
- 32х + 4у = - 52
32х + 7у = 61
11у = 9
у = 9/11
8х - 8/11 = 13
х = 19/11
х = 19/11 ; у = 9/11