Question

Решите неравенство а)5х<20 в)8х>-16 д)1/4x<1
б)-2х<-6 г)-7х>21 e) -1/3x>2
Укажите какие-нибудь два решения неравенства

Answer 1

а)5х<20

х<20:5

х<4

(-∞; 4)

б)-2х<-6

х>-6:(-2)

х>3

(3; ∞)

в)8х>-16

х>-16:8

х>-2

(-2; +∞)

г)-7х>21

х<21:(-7)

х<-3

(-∞; -3)

д)1/4x≤1

х≤1:1/4

х≤4

(-∞; 4]

e) -1/3x≥2

х ≤ 2:(-1/3)

х ≤ 2*(-3)

х ≤ -6

(-∞; -6]

Answer 2

Объяснение:

a) 5x < 20  

x < 4    

x = 0; 3 (любые два решения неравенства)

б) -2x < -6

  x > -6 / -2

   x > 3

   x = 4; 6 (любые два решения неравенства)

в) 8x > -16

   x > -2

   x = -1; 0 (любые два решения неравенства)

г) -7x > 21

    x < 21 / -7

    x < -3

    x = -4; -6 (любые два решения неравенства)

д) 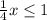$\frac{1}{4} x \leq 1$

   x ≤ 4 * 1

   x ≤ 4

   x = 2; 4 (любые два решения неравенства)

е) 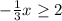$-\frac{1}{3} x \geq 2$

     x ≤ 2 * (-3)

     x ≤ - 6

     x = -8; -6 (любые два решения неравенства)