Составьте математическую модель задачи и решите ее: Катер 30 км против течения реки и 12 км по течению за то же время, за которое он может пройти по озеру 44 км. Определите скорость катера по озеру, если скорость течения реки составляет 2 км/ч.
1) Так как трапеция ABCD равнобокая и в неё вписана окружность, то её боковые стороны будут равны средней линии трапеции, т.е. AB=CD=m, где m===12,5. ⇒ AB=CD=12,5.
2) Проведём из точек В и С перпендикуляры к стороне AD. ⇒ BH₁=CH ⇒ AH₁=HD==3,5.
3) Рассмотрим прямоугольный треугольник ABH₁. И по теореме Пифагора найдём высоту трапеции ABCD, т.е. BH₁. ⇒
⇒ BH₁=====12.
4) Площадь трапеции равна S=, где m - сред.линия; h - высота трапеции. ⇒ S==6,25*12=75.
5) Так как в трапецию вписана окружность, то её площадь равна S=pr, где p - полупериметр трапеции; r - радиус вписанной окружности.
Под методом математической индукции понимают следующий доказательства. Если требуется доказать истинность предложения А(n) для всех натуральных n, то, во-первых, следует проверить истинность высказывания А(1) и, во-вторых, предположив истинность высказывания А(k), попытаться доказать, что высказывание А(k+1) истинно. Если это удается доказать, причем доказательство остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(n) признается истинным для всех значений n.
r=3.
Объяснение:
1) Так как трапеция ABCD равнобокая и в неё вписана окружность, то её боковые стороны будут равны средней линии трапеции, т.е. AB=CD=m, где m=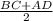 =
=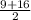 =12,5. ⇒ AB=CD=12,5.
=12,5. ⇒ AB=CD=12,5.
2) Проведём из точек В и С перпендикуляры к стороне AD. ⇒ BH₁=CH ⇒ AH₁=HD=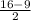 =3,5.
=3,5.
3) Рассмотрим прямоугольный треугольник ABH₁. И по теореме Пифагора найдём высоту трапеции ABCD, т.е. BH₁. ⇒
⇒ BH₁=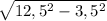 =
=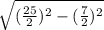 =
=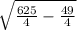 =
=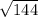 =12.
=12.
4) Площадь трапеции равна S=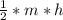 , где m - сред.линия; h - высота трапеции. ⇒ S=
, где m - сред.линия; h - высота трапеции. ⇒ S=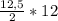 =6,25*12=75.
=6,25*12=75.
5) Так как в трапецию вписана окружность, то её площадь равна S=pr, где p - полупериметр трапеции; r - радиус вписанной окружности.
⇒ p=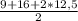 =25. ⇒ 75=25*r ⇒ r=
=25. ⇒ 75=25*r ⇒ r=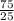 =3.
=3.