Считать будем все броски подряд, из которых нечетные (1, 3, 5) делает первый игрок, а четные (2, 4, 6) - второй.
Первый побеждает в следующих ситуациях:
- попал 1 броском
- попал 3 броском, а все предыдущие броски закончились промахом
- попал 5 броском, а все предыдущие броски закончились промахом
Второй побеждает в следующих ситуациях:
- попал 2 броском, а предыдущий бросок закончился промахом
- попал 4 броском, а все предыдущие броски закончились промахом
- попал 6 броском, а все предыдущие броски закончились промахом
Зная вероятность попадания 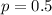 , вычислим вероятность промаха:
, вычислим вероятность промаха:
 :
:
Вероятность победы первого игрока:
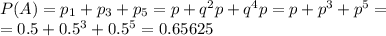
Вероятность победы второго игрока:
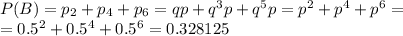
ответ: победа первого с вероятностью 0.65625, победа второго с вероятностью 0.328125
Объяснение:
Формула разности квадратов а²-в²=(а-в)(а+в) ;
(а-в)²=(в-а)²
6) ( 2х-о,5у)²-(х-у)²= ( ( 2х-о,5у)- (х-у) ) ( ( 2х-о,5у) + (х-у) )=
= ( 2х-о,5у- х+у ) ( 2х-о,5у + х-у )=(х-0,5у)(3х-1,5у)=
=1,5(х-0,5у)(2х-у)
7) (5а-2)³+(2-5а)²= (5а-2)³+1*(5а-2)²= вынесем общий множитель за скобку=(5а-2)²(5а-2+1)=(5а-2)²(5а-1).
8)( 0,2а-в)²-(а-0,2в)²= формула разности квадратов=
=( ( 0,2а-в)-(а-0,2в) )( ( 0,2а-в)+(а-0,2в) )=
=( 0,2а-в-а+0,2в )( 0,2а-в+а-0,2в )=(-0,8а-0,8в)(1,2а-1,2в)=
=-0,8*1,2(а+в)(а-в)=-0,96(а+в)(а-в).
9) аналогично 7 ( см в комментариях)
10) 1,21х²-0,36у⁶=(1,1х)²-(0,6у³)²= разность квадратов=
=(1,1х-0,6у³)( 1,1х+0,6у³).
11)2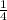 *а⁴ -
*а⁴ -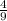 *в²=
*в²=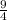 а⁴ -
а⁴ -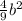 =
=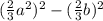 =
=
=(1,5a²-2/3в²) (1,5a²+2/3в²).
12) 1,69х⁸y⁸-9=(1,3х⁴у⁴)²-3²= (1,3х⁴у⁴-3) (1,3х⁴у⁴+3)
ответ смотри на фотографии