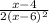1)Найдем производную,приравняем к 0,чтобы найти критические точки.Определим знаки на интервалах,для определения убывания и возрастания. f`(x)=3x²-12x-36=3(x²-4x-12)=0 (x²-4x-12)=0 по теореме Виета x1+x2=4 U x1*x2=-12⇒x1=-2 U x2=6 + _ + ________________________________________ возр -2 Убыв 6 возр возр x∈(-≈;-2) U (6;≈) 2)При нахождении первообразной степень увеличиваем на 1 и на этот показатель делим неизвестное F(x)= - 6 - 3x+C= - 2[tex] x^{3} - 3x+C 3)Делаем тоже самое , что в 1.Смена знака с минуса на плюс-минимум f`(x)=4 -1/x=(4x-1)/x=0 4x-1=0⇒4x=1⇒x=1/4 _ + _____________________ 1/4 min ymin(1/4)=4*1/4-ln1/4+1=1-ln1+ln4+1=2+ln4 (1/4;2+ln4)
1 уравнение
6/х^2-36 + 1/36-12x + x^2 + 1/2x+12 - 0
6/(x-6) * (x+6) + 1/(6-x)^2 + 1/2(x+6)
6/(x-6)*(x+6) + 1/(-(x-6))^2 + 1/2(x+6)
12(x-6)+2(x+6)+(x-6)^2 / 2(x-6)^2*(x+6)
14x-60+x^2-12x+36/2(x-6)^2 * (x+6)
2x-24+x^2/2(x-6)^2 * (x+6)
x^2 + 6x-4x-24/2(x-6)^2 * (x+6)
(x+6)*(x-4)/2(x-6)^2*(x+6)
ответ;