У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Пусть печенья купили х кг, а конфет - у кг, тогда можно записать систему уравнений: В первом уравнении показали что сумма печенья и конфет равна 38 кг, а во втором показали что сумма стоимости конфет и стоимости печенья равна 2080 руб. (стоимость печенья 50*х, а стоимость конфет 60*у). Решаем систему уравнений, выразим х через у и подставим во второе уравнение; Нашли сколько купили конфет - 18 кг. Теперь найдём сколько купили печенья: x+18=38 x=38-18 x=20 (кг)
Правильное условие такое:
У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Решение.
ОДЗ: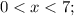
Методом подбора быстрее.
1) Начнем с решения второго уравнения.
Если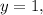
то 7-1=6. Тогда 
не натуральное число.
Если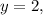
то 7-2=5. Тогда 
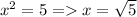не натуральное число.
Если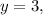
то 7-3=4. Тогда 
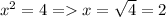натуральное число.
Получили решение
2) Подставим
в первое уравнение 
.
ответ: 2 груши у брата;
3 яблока у сестры.