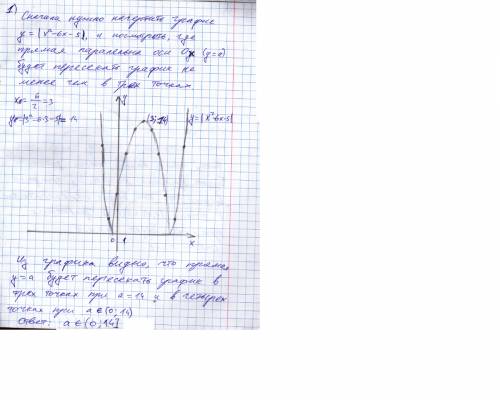
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,
а нижнее а=0.
находим вершину параболы, х0=-b/2a у нам b=6 a=-1 x0=3
y0=-9+5+18=14
значит а [0;14]
2) sqrt(x-1)=a+x x>=1
x-1=x^2+a^2+2ax
x^2+(2a-1)x+a^2+1=0
D>0 (2a-1)^2-4a^2-4>0 -4a-3>0 a<-3/4
3) 4x^2-15x+4a^3=0
x1=x2^2
x1*x2=a^3
x2^3=a^3 x2=a
15/4=x1+x2 15/4=a^2+a
4a^2+4a-15=0 a1=3/2 a2=-5/2
x^2-ax+(a-1)=0
x1^2+x2^2=(x1+x2)^2-2x1x2=17
a^2-2(a-1)=17
a^2-2a-15=0
a1=5 a2=-3



Р = 60 см
Объяснение:
Пусть гипотенуза - х см,тогда один катет х-16 см,а другой х-2 см
Сумма квадратов катетов равна квадрату гипотенузы, поэтому
(х-16)²+(х-2)²= х²
х²-32х+256+х²-4х+4 = х²
х²-36х+260 = 0
D = (-36)²-4*260 = 1296 - 1040 = 256 = 16²
x12 = (36±16)/2
x1 = 26
x2 = 10
Второй корень меньше 16,поэтому он нам не подходит(10-16 = -6,а длина не может быть отрицательной)
Проверим оставшийся корень
Если гипотенуза равна 26 см,то один катет равен 10 см,а другой 24 см
10²+24²=26²
100+576 = 676
676 = 676
Р = 10+24+26 = 60 см
Верно