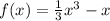
1)
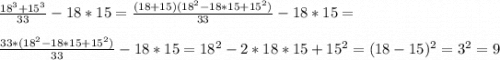
2)
2x³-54=2*(x³-27)=2*(x³-3³)=2*(x-3)(x²-3x+9)
3) а
(3х-4)²+(2х-4)(2х+4)+65х=
9х²-24х+16+4х²-16+65х=
13х²+41х=x(13x+41)
b)
при x=-3
x*(13x+41)= -3*(13*(-3)+41)=-3*(-39+41)=-3*(-2)=-6
4)
х-первое число
у-второе число
х²-у²=52}
х+у=26 }
(x-y)(x+y)=52 (1)
(x+y)=26 подставим в (1) ,получим
(х-у)*26=52} сократим на 26
х+у=26 }
x-y=2 }
x+y=26 } сложим левые и правые части
----------------------------------------
х+х-у+у=26+2
2х=28
х=28:2
х=14 подставим в x-y=2 получим
14-у=2
у=12
ответ: числа 12 и 14.
Определение локального максимума и локального минимума
Пусть функция
y
=
f
(
x
)
определена в некоторой
δ
-окрестности точки
x
0
,
где
δ
>
0.
Говорят, что функция
f
(
x
)
имеет локальный максимум в точке
x
0
,
если для всех точек
x
≠
x
0
,
принадлежащих окрестности
(
x
0
−
δ
,
x
0
+
δ
)
,
выполняется неравенство
f
(
x
)
≤
f
(
x
0
)
.
Если для всех точек
x
≠
x
0
из некоторой окрестности точки
x
0
выполняется строгое неравенство
f
(
x
)
<
f
(
x
0
)
,
то точка
x
0
является точкой строгого локального максимума.
Аналогично определяется локальный минимум функции
f
(
x
)
.
В этом случае для всех точек
x
≠
x
0
из
δ
-окрестности
(
x
0
−
δ
,
x
0
+
δ
)
точки
x
0
справедливо неравенство
f
(
x
)
≥
f
(
x
0
)
.
Соответственно, строгий локальный минимум описывается строгим неравенством