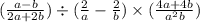
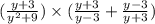
В решении.
Объяснение:
1. Дана функция: у = 1/3 х² → у = х²/3;
График - парабола, ветви направлены вверх. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -6 -3 0 3 6
у 12 3 0 3 12
По вычисленным точкам построить параболу.
2. Дана функция у = 1/2 х² - 1 → у = 0,5х² - 1;
График - парабола, ветви направлены вверх, центр смещён по оси Оу вниз на 1 единицу. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -4 -3 -2 -1 0 1 2 3 4
у 7 3,5 1 0,5 -1 -0,5 1 3,5 7
По вычисленным точкам построить параболу.
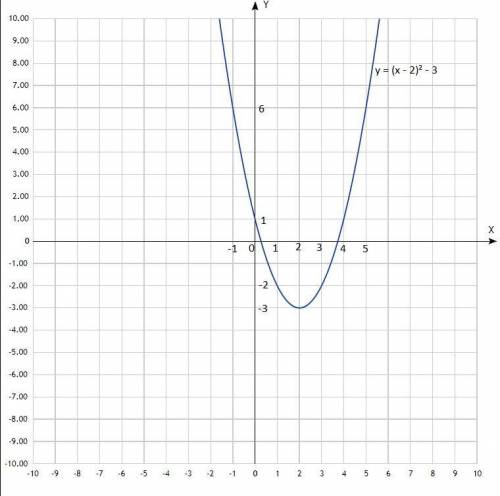
3. Дана функция у = -3 + (х - 2)² → у = (х - 2)² - 3;
График - парабола, ветви направлены вверх, центр смещён по оси Ох вправо на 2 единицы и по оси Оу вниз на 3 единицы. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2 3 4 5 6
у 13 6 1 -2 -3 -2 1 6 13
По вычисленным точкам построить параболу.
В решении.
Объяснение:
1. (0,4m + n⁴)(0,16m² - 0,4mn⁴ + n⁸) =
= 0,064m³ - 0,16m²n⁴ + 0,4mn⁸ + 0,16m²n⁴ - 0,4mn⁸ + n¹² =
= 0,064m³ + n¹².
2. 68,4² − 68,3² = разность квадратов, разложить по формуле:
= (68,4 - 68,3)*(68,4 + 68,3) =
= 0,1 * 136,7 = 13,67.
3. Разложи на множители:
36t² + 84t + 49 = (6t + 7)² = (6t + 7)*(6t + 7).
Выбери все возможные варианты:
(6t+7)⋅(6t+7)
(6t−7)⋅(6t−7)
(6t−7)2
(6t+7)⋅(6t−7)
4. Представь квадрат двучлена в виде многочлена:
(18x⁴ − 34)² = квадрат разности, разложить по формуле:
= 324х⁸ - 1224х⁴ + 1156.
Ущвлатаьпдпзшрш