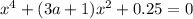
Заменим x^2 на t , t ≥ 0:
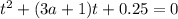
Начальное уравнение будет иметь два корня,
только если уравнение 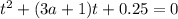будет иметь только один корень, который больше нуля или один из корней будет < 0 , а другой > 0.
Рассмотрим эти два случая :
1. Уравнение будет иметь один корень, если D = 0 :
[ 
=> 
[ 
=> 
=> 
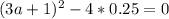
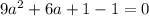
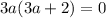
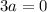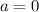
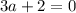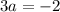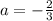
a = 0 не подходит, т.к при а = 0, уравнение имеет корень -0.5, а он < 0.
2. Один из корней уравнения будет < 0 , а другой > 0, если :
{ D > 0
{ f(0) < 0 , где f(t) = t^2 +(3a+1)t+0.25=0
-----------------
{ 
{ 
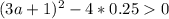
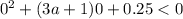=> 0.25 < 0 => x ∈ ∅
ответ : при a = -2/3
Биквадратное уравнение.
Решается заменой переменной:
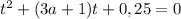
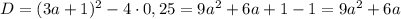
Если D >0, т.е.
уравнение имеет корни:
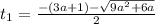или 
Обратный переход:
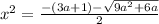или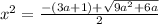 
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
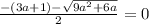
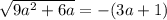
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Аналогично
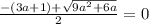
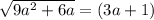
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Если 
, т.е 
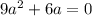
или 
При
уравнение принимает вид:
⇒ 
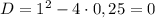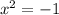
уравнение не имеет корней
При
уравнение принимает вид:
⇒ 
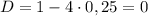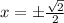
Уравнение 4-ой степени, значит
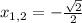и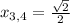 
О т в е т. При
tg 30 = x / 88
x = 88 * tg 30
площадь равна произведению катетов пополам
S = 88 * 88 * tg 30 /2 = 1/2 * 88^2 tg 30