см, тогда второй катет - 
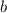см. Площадь прямоугольного треугольника равна 
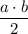, что составляет 210 см² или перепишем сразу 
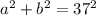
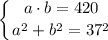
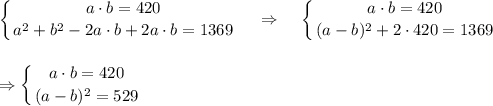
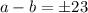. Тогда имеем несколько случаев.
, то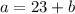 
и подставим в первое уравнение.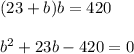
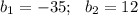см и корень 
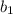не удовлетворяет заданному условию
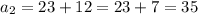см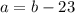
,то подставив в первое уравнение, получим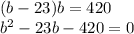
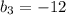
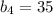см и корень 
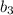не удовлетворяет условию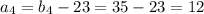
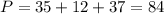см
1)найти стационарные точки
f(x)=x^4-200x^2+56
f`(x) = 4x³ - 400x
4x³ - 400x = 0
4x*(x² - 100) = 0
4x = 0, x₁ = 0
x² - 100 = 0
x² = 100
x₂ = - 10
x₃ = 10
ответ: x₁ = 0 ; x₂ = - 10 ; x₃ = 10 - стационарные точки
2) определить интервалы возрастания функций
f(x)=x^3-x^2-x^5+23
1. Находим интервалы возрастания и убывания.
Первая производная.
f'(x) = -5x⁴ + 3x² - 2x
или
f'(x) = x * (-5x³ + 3x - 2)
Находим нули функции.
Для этого приравниваем производную к нулю
x * (-5x³ + 3x - 2) = 0
Откуда:
x₁ = - 1
x₂ = 0
(-1; 0) f'(x) > 0 функция возрастает
3) определить интервалы убывания функций
f(x)=x^3-7,5x^2+1
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 3x² - 15x
или
f'(x) = x*(3x - 15)
Находим нули функции. Для этого приравниваем производную к нулю
x*(3x - 15) = 0
Откуда:
x₁ = 0
x₂ = 5
(0; 5) f'(x) < 0 функция убывает
4) вычислить значение функции в точке максимума
f(x)=x^3-3^2-9x+1
Решение.
Находим первую производную функции:
y' = 3x² - 9
Приравниваем ее к нулю:
3x² - 9 = 0
x² = 3
x₁ = - √3
x₂ = √3
Вычисляем значения функции
f(- √3) = - 8 + 6√3 точка максимума
f(√3) = - 6√3 - 8
fmax = - 8 + 6√3
ответ: fmax = - 8 + 6√3