Пусть двузначное число составлено из двух цифр a и b, причём a≠0 и b≠0. Тогда число можно представить в виде суммы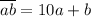 
.
Сразу проверим случай a=b : 
. Так как число 11 - простое (делители 1 и 11), только число 11 будет кратно 1·1. Другие двузначные числа не подходят под условие.
Число кратно произведению цифр ab.
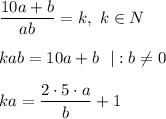
Так как числа ka и 1 - целые, значит, дробь должна тоже стать целым числом. Знаменатель b должен быть равен 1 или сократиться.
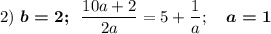
4) Число a или число 2a должны быть кратны цифре b. Возможные пары, помимо рассмотренных : (2;4), (3,6), (4,8), (6,3), (8,4), (9,3)
a = 2; b = 4; 
a = 3; b = 6;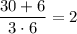 
Остальные варианты не подходят
a = 4; b = 8;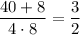 
a = 6; b = 3; 
a = 8; b = 4; 
a = 9; b = 3; 
ответ : 11, 12, 15, 24, 36
В решении.
Объяснение:
1) Построить график у = 2х + 5.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у 3 5 7
При х = 1 у = 7;
При х = -0,5 у = 4.
2) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
у = 3х + 4; А(0; 4); В(1; 7).
а) 4 = 3*0 + 4
4 = 4, принадлежит;
б) 7 = 3*1 + 4
7 = 7, принадлежит.
3) у = -2х + 1
у = х + 4
-2х + 1 = х + 4
-2х - х = 4 - 1
-3х = 3
х = -1;
у = х + 4
у = -1 + 4
у = 3.
Координаты точки пересечения прямых (-1; 3).