Объяснение:
a) x² - 2x - 15 < 0
x² + 3x - 5x - 15 > 0
x(x + 3) - 5(x + 3) > 0
(x + 3)(x - 5) > 0
x + 3 < 0 x - 5 > 0
x < -3 x > 5
x ∈ (-∞, -3) ∪ (5, +∞)
б) -x² + 6x ≥ 0
-x(x - 6) ≥ 0
x(x - 6) ≤ 0
x ≥ 0 x - 6 ≤ 0
x ≤ 6
x ∈ [0, 6]
в)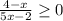 
4 - x ≤ 0 5x - 2 > 0
x ≤ 4 5x > 2
x >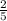 
x ∈ (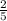, 4]
г) x(x - 9)(x + 2) > 0
x < 0 (x - 9)(x + 2) > 0
x - 9 > 0 x + 2 > 0
x > 9 x > -2
x ∈ (-2, 0) ∪ (9, +∞)
д)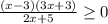 
2x + 5 > 0 (x - 3)(3x + 3) ≥ 0
2x > -5 x - 3 ≥ 0 3x + 3 ≤ 0
x >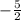 
x ≥ 3 3x ≤ -3
x ≤ -1
x ∈ (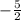 , -1] ∪[3, +∞)
p=m/n
n=90 ( количество двузначных чисел)
Числа делящиеся на 3:
12; 15;... 99 - таких чисел 30
Можно найти их количество по формуле n-го члена арифметической прогрессии
a₁=12
d=15-12=3
99=12+3·(n-1) ⇒87=3(n-1) n-1=29 n=30
Числа делящиеся на 5:
10; 15;20; 25; 30;...; 95 - таких чисел 30
Можно найти их количество по формуле n-го члена арифметической прогрессии
a₁=10
d=15-10=5
95=10+5·(n-1) ⇒85=5(n-1) n-1=19 n=20
Чисел, которые одновременно делятся и на 3 и на 5 всего 6:
15;30;45;60;75 и 90
m=30+20-6=44
p=44/90=22/45