Задача : Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места.
Решение: Вероятность набрать верную цифру из десяти равна по условию 1/10. Рассмотрим следующие случаи:
1. первый звонок оказался верным, вероятность равна 1/10 (сразу набрана нужная цифра).
2. первый звонок оказался неверным, а второй - верным, вероятность равна 9/10*1/9=1/10 (первый раз набрана неверная цифра, а второй раз верная из оставшихся девяти цифр).
3. первый и второй звонки оказались неверными, а третий - верным, вероятность равна 9/10*8/9*1/8=1/10 (аналогично пункту 2).
Всего получаем P=1/10+1/10+1/10=3/10=0,3P=1/10+1/10+1/10=3/10=0,3 - вероятность того, что ему придется звонить не более чем в три места.
ответ: 0,3
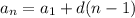
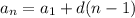
В решении.
Объяснение:
6. Решите систему неравенств:
x² - 8x + 25 > 0
х² - 49 ≤ 0
Решить первое неравенство:
x² - 8x + 25 > 0
Приравнять к нулю и решить квадратное уравнение:
x² - 8x + 25 = 0
D=b²-4ac =64 - 100 = -36
D < 0
Уравнение не имеет действительных корней.
Значит, неравенство выполняется всегда или не выполняется никогда.
Подставить в неравенство произвольное значение х:
х = 0;
0 - 0 + 25 > 0, выполняется.
Значит, неравенство верно при любом значении х.
Решение первого неравенства: х∈(-∞; +∞).
Решить второе неравенство:
х² - 49 ≤ 0
Приравнять к нулю и решить квадратное уравнение:
х² - 49 = 0
х² = 49
х = ±√49
х₁ = -7;
х₂ = 7.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -7 и х= 7.
Решение второго неравенства: х∈[-7; 7].
Неравенство нестрогое, скобки квадратные.
Отметить на числовой оси интервалы решений двух неравенств и найти пересечение решений (решения, которые подходят двум неравенствам).
Решение первого неравенства: х∈(-∞; +∞). Штриховка по всей числовой оси.
Решение второго неравенства: х∈[-7; 7]. Штриховка от х = -7 до х = 7.
Пересечение решений (двойная штриховка): х∈[-7; 7].