Решить неравенства:
1)
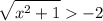
определим ОДЗ:
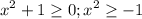
т.е. неравентсво определено на всем множестве R
Подкоренное выражение всегда ≥0. А значит решением данное неравенства будет множество R
ответ: x∈R
2)
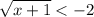
определим ОДЗ:
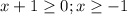
Значит неравенство имеет смысл если х∈[-1;+∞)
Но при этом √x+1 ≥0 и ни когда не будет отрицательным числом, а значит неравенство не выполнимо
ответ: x∈∅
3)
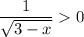
определим ОДЗ:
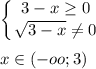
При допустимых х выражение √3-x>0; и значит дробь тоже принимает положительные значения
ответ: x∈(-∞;3)
4)
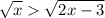
определим ОДЗ:

значит допустимые значения х∈[1.5; +∞)
т.к. с обеих сторон стоят положительные числа то можем данное неравенство возвести в квадрат

по решению х<3
совместим с ОДЗ
ответ: x∈[1.5; 3)
(умножив обе части неравенства на (-1
(3x^2 - 4x + 5) / (2x+3) < 0
теперь найти корни для числителя
для знаменателя корень (-3/2)
D = 16-4*3*5 < 0 ---> квадратный трехчлен не имеет корней, значит
"парабола--ветви вверх" (((это график кв.трехчлена))) не пересекает ось ОХ,
а т.к. "ветви вверх" --- она всегда только выше оси ОХ,
т.е. функция ((выражение в числителе))) всегда строго больше нуля)))
числитель всегда > 0, а дробь должна быть < 0
делаем вывод, что знаменатель < 0
это неравенство равносильно неравенству: 2x+3 < 0
x < -1.5
это ответ)))