Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
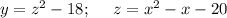
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
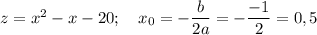 - координата вершины
- координата вершины
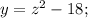 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
а) например, 1236 и 1241.
б) наименьшее из таких двух чисел не может оканчиваться на 9 или иметь в разряде десятков 1, в противном случае в большем числе появился бы 0. Значит, эти числа должны выглядеть так: a b c d и a b+1 c-1 d+1. Из условия следует, что сумма цифр любого интересного числа четная, а суммы цифр этих двух чисел отличаются на (a + b + 1 + c - 1 + d + 1) - (a + b + c + d) = 1 и не могут быть одновременно чётными.
в) 9135 делится на 1, 3, 5 и 7; 1719 делится на 9. Докажем, что не бывает интересных чисел, делящихся на 11.
Признак делимости на 11: число делится на 11, если и только если разность сумм цифр на чётных и нечётных местах делится на 11; число a b c d делится на 11, если (a + c) - (b + d) делится на 11.
Поскольку сумма всех цифр четная, a сумма двух цифр не превосходит 18, то a + c = b + d.
Если максимальная из цифр a или c, то она меньше, чем сумма b + d; если она b или d, то, соответственно, меньше a + c. Поэтому максимальная из цифр не может оказаться равной сумме оставшихся цифр.
ответ. а) 1236 и 1241, б) нет, в) 11
среднее арифметическое это число, равное сумме всех чисел множества, делённой на их количество.
Мода это значение во множестве наблюдений, которое встречается наиболее часто
мода равна 2 и 3 т.к оба встречаются 3 раза
размах называется разность между наибольшим и наименьшим из чисел этого ряда.
наибольшее 3, наименьшее 2
3-2=1
Медиана - это значение приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака,
сначала разместим числа в порядке возрастания
2,2,2,3,3,3
видно что чисел шесть тогда медиана равна среднему аримфметическому двух средних чисел
(если допустим было нечетное количество тогда медиана была равна среднему числу. Пример 2,2,2,3,3,3,3 - медиана равна 3)