
Задание 1. - вложение 1
а) (x+9)(x-5)>0
f(x)=(x+9)(x-5)
Нули функции: -9; 5
ответ: (-∞; 9)∪(5; +∞)
б)
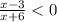
ОДЗ: x≠-6
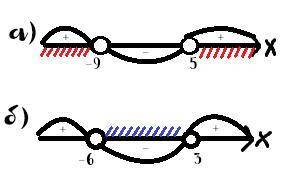
(x-3)(x+6)<0
f(x)=(x-3)(x+6)
Нули функции: 3; -6
ответ: (-6; 3)
Задание 2.
а)
x³ - 49x = 0
x(x²-49)=0
x(x-7)(x+7)=0
x=0 или x=7 или x=-7
ответ: -7; 0; 7
б)
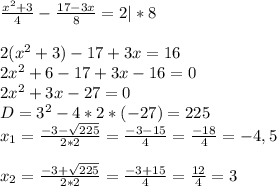
ответ: -4,5; 3
в) x⁴ - 17x² + 16 = 0
x² = t - новая переменная
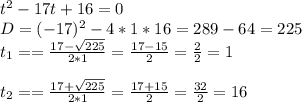
x² = 1 или x² = 16
x₁=-1 ; x₂=1 ; x₃=-4 ; x₄=4
ответ: ±1; ±4
Задание 3. - вложение 2
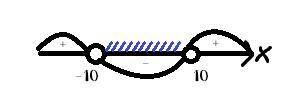
D < 0, корней нет
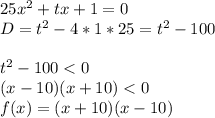
Нули функции: 10; -10
ответ: t∈(-10; 10)
Задание 4. - вложение 3
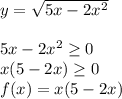
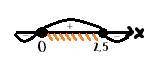
Нули функции: 0; 2,5
ответ: x∈[0; 2,5]
б) c3=c2*q=12*(-4)=-48
в) c(n)=c1*q^(n-1)=-3*(-4)^(n-1)=3/4*(-4)^n
г) c6=3/4*(-4)^6=3*4^5=3*1024=3072
д) Так как для произвольного члена прогрессии c(n) не выполняется ни равенство с(n+1)>c(n), ни равенство c(n+1)<c(n), то прогрессия не является ни возрастающей, ни убывающей.
e) Это прогрессия -3, -12, -48,, т.е. прогрессия c c1=-3 и знаменателем q=4
ж) Одна, указанная выше. Другие прогрессиии имеют другой знаменатель q, поэтому даже если у них с1=-3, то другие члены с нечётными номерами не будут совпадать с членами данной прогрессии.