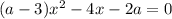
можно решить двумя смотря в каком ты классе ну ты поймешь какой тебе вариант подойдет
Первый учитель проверяет 360:15=24 тетради в час, второй 360:10=36 тетрадей, третий 360:6=60 тетрадей, вместе будет 360:(24+36+60)=3часа
2 вариант решения:
1 учитель делает всю работу за 15 часов, а за один час он сделает 1/15 часть работы, второй сделает за один час 1/10 часть, а третий 1/6 часть. Тогда втроём за один час они сделают 1/15 + 1/10 + 1/6 = 2/30 + 3/30 + 5/30 = 10/30= 1/3 часть. Тогда всю работу они сделают за 1 : 1/3 = 1 * 3 = 3 часа ответ 3 ч потребуется на проверку всех тетрадей
ответ: 1) 10; 2) 8; 3) 11; 4) 12;
Объяснение:
1) Ребро куба х, его объём х³
Ребро куба, после увеличения на 2 станет (х+2),а объём куба после увеличения ребра на 2 станет (х+2)³
Так как объём куба увеличился на 728, то (х+2)³-х³=728
Решим это уравнение (х+2)³-х³=728
х³+3·х²·2+3·х·2²+2³-х³=728
6х²+12х+8=728
6х²+12х-720=0
х²+2х-120=0
По теореме, обратной теореме Виета х1=-12( не подх); х2=10
ответ:10
2) Ребро куба х, его объём х³
Ребро куба, после увеличения на 3 станет (х+3),а объём куба после увеличения ребра на 3 станет (х+3)³
Так как объём куба увеличился на 728, то (х+3)³-х³=819
Решим это уравнение (х+3)³-х³=819
х³+3·х²·3+3·х·3²+3³-х³= 819
9х²+27х+27=819
9х²+27х-792=0
х²+3х-88=0
По теореме, обратной теореме Виета х1=-11( не подх); х2=8
ответ:8
3) Ребро куба х, его объём х³
Ребро куба, после увеличения на 3 станет (х+3),а объём куба после увеличения ребра на 3 станет (х+3)³
Так как объём куба увеличился на 728, то (х+3)³-х³=1413
Решим это уравнение (х+3)³-х³=1413
х³+3·х²·3+3·х·3²+3³-х³= 1413
9х²+27х+27=1423
9х²+27х-1386=0
х²+3х-154=0
По теореме, обратной теореме Виета х1=-14( не подх); х2=11
ответ:11
2) Ребро куба х, его объём х³
Ребро куба, после увеличения на 1 станет (х+1),а объём куба после увеличения ребра на 1 станет (х+1)³
Так как объём куба увеличился на 728, то (х+3)³-х³=819
Решим это уравнение (х+1)³-х³=721
х³+3·х²·1+3·х·1²+1³-х³= 721
3х²+3х+1=721
3х²+3х-720=0
х²+3х-240=0
По теореме, обратной теореме Виета х1=-10( не подх); х2=12
ответ:12
a=2 или a=1
Объяснение:
Уравнение имеет единственный корень если дискриминант равен 0.
D=16+8a(a-3)=16+8a^2-24a=8*(a^2-3a)+16=8*(a-1,5)^2+16-8*3*3/4=
8*(a-1,5)^2+16-18=0
(a-1,5)^2=1/4
a=2 или a=1