 ;
;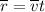 ;
;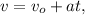 либо в векторном виде:
либо в векторном виде: 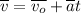 ;
;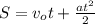 либо в векторном виде:
либо в векторном виде: 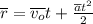 ;
;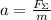 либо в векторном виде:
либо в векторном виде: 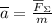 ;
; ;
;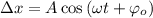 ;
;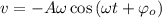 ;
; ;
;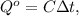 где
где 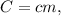 либо в удельном виде:
либо в удельном виде:  ;
;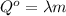 ;
;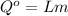 ;
; ;
; ;
;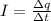 ;
;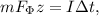 где
где  ;
;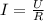 ;
;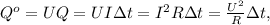
 ;
;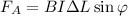 ;
; ;
;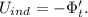
В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение: 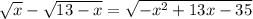
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части: 
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень 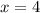
(3;0)
Объяснение:
Метод постановки:
: х=3-у
3(3-у)+3=4(3-у)-2у
9-3у+3=12-4у-2у
12-3у=12-6у
-3у+6у=12-12
3у=0
у=0:3
у=0
х=3-у
х=3-0
х=3
: у=3-х
3х+3=4х-2(3-х)
3х+3=4х-6+2х
3х+3=6х-6
3х-6х=-3-6
-3х=-9
х=-9:(-3)
х=3
у=3-х
у=3-3
у=0
Метод сложения:
3х+3=4х-2у
х+у=3
3х-4х+2у=-3
х+у=3
2у-х=-3 2у-х=-3
+
х+у=3|×2 2х+2у=6
х=3
х+у=3
3+у=3
у=3-3
у=0
ИЛИ
2у-х=-3
2у-3=-3
2у=3+(-3)
2у=0
у=0:2
у=0
Графический метод делается с чертежом и таблицей, уже расписывать не стала)