Алгебра: При x -3 значение функции y=ax^2 равно -9 найдитезначение a

При x -3 значение функции y=ax^2 равно -9 найдитезначение a

👇

Ответ:

kriskuziya0708

05.05.2023

При x -3 значение функции y=ax^2 равно -9
При x= -3 значение функции y= -9
Из функции у=ax^2 а=у/x^2 a=-9/(-3)^2= -9/9= -1
ответ а= -1

4,8(97 оценок)

Открыть все ответы

Ответ:

BestPe

05.05.2023

Объяснени

Физика, 17.09.2020 12:46, inan228

Вопрос 1 Кому принадлежат данные высказывания? Варианты ответов 1. Тело падает на Землю тем быстрее, чем больше его масса. 2. Все тела падают на Землю с одинаковым ускорением. Вопрос 2 Если все тела падают с одинаковым ускорением, то почему перо падает медленнее камня? Варианты ответов 1. Потому что масса камня больше массы пера. 2. Потому что на перо действует сила сопротивления воздуха, сравнимая с силой тяжести. 3. что на самом деле не все тела падают с одинаковым ускорением. 4. Потому, что сила тяжести, действующая на камень, гораздо больше силы сопротивления воздуха. Вопрос 3 Выберете верные утверждения о теле, находящемся в свободном падении. Варианты ответов 1. Это тело испытывает состояние невесомости. 2. Это тело находится в космосе. 3. Это тело двигается только под действием силы тяжести. 4. Это тело испытывает перегрузки. Вопрос 4 Камень бросают с обрыва под углом 45о к горизонту. Модуль начальной скорости равен 3 м/с, а высота обрыва составляет 50 м. Найдите время полёта камня (в с) до момента удара о землю и расстояние (в м), которое он пройдёт за это время. g = 10 м/с2. ответы округлите до десятых. ответ запишите в указанном порядке через точку с запятой без единиц измерения (например, 1,1; 2,2). Вопрос 5 Какой высоты достигнет тело, брошенное вертикально вверх с начальной скоростью 10 м/с? Варианты ответов 1. 5 м 2. 10 м 3. 0,5 м 4. 15 м Вопрос 6 Найдите время (в с), за которое тело упадёт с высоты 15 м, предполагая, что тело изначально покоилось (g = 10 м/с2), а также его скорость (в м/с) в момент удара о землю. ответы округлите до десятых. ответ запишите в указанном порядке через точку с запятой без единиц измерения (например, 1,1; 2,2). Вопрос 7 Что отсутствует у тела при его свободном падении? Вопрос 8 От чего зависит ускорение свободного падения? Варианты ответов 1. От массы планеты. 2. От высоты над поверхностью планеты. 3. От плотностие:

4,7(26 оценок)

Ответ:

браинли56

05.05.2023

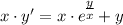
$x\cdot y'=x \cdot e^\big{ \frac{y}{x} }+y$
Убедимся, что данное дифференциальное уравнение является однородным.

То есть, воспользуемся условием однородности
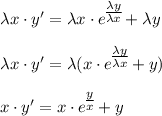
$\lambda x\cdot y'=\lambda x \cdot e^\big{ \frac{\lambda y}{\lambda x} }+\lambda y\\ \\ \lambda x\cdot y'=\lambda(x \cdot e^\big{ \frac{\lambda y}{\lambda x} }+y)\\ \\ x\cdot y'=x \cdot e^\big{ \frac{y}{x} }+y$
Итак, данное дифференциальное уравнение является однородным.

Однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u=u(x)

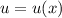с замены:

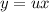, тогда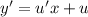

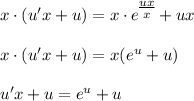
$x\cdot (u'x+u)=x\cdot e^\big{ \frac{ux}{x} }+ux\\ \\ x\cdot (u'x+u)=x(e^u+u)\\ \\ u'x+u=e^u+u$

u'x=e^u

По определению дифференциала, получаем
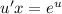
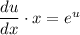$\dfrac{du}{dx} \cdot x=e^u$ - уравнение с разделяющимися переменными.
Разделим переменные.
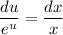$\dfrac{du}{e^u} = \dfrac{dx}{x}$ - уравнение с разделёнными переменными.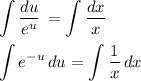

Проинтегрируем обе части уравнения
$\displaystyle \int\limits { \frac{du}{e^u} } \,=\int\limits { \frac{dx}{x} } \\ \\ \int\limits {e^{-u}} \, du=\int\limits { \frac{1}{x} } \, dx$
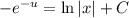$-e^{-u}=\ln |x|+C$ - общий интеграл новой функции.

Таким образом, определив функцию

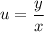
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: $u= \dfrac{y}{x}$

То есть,

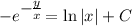$-e^\big{-\frac{y}{x} }=\ln |x|+C$ - общий интеграл исходного уравнения.
Остаётся определить значение произвольной постоянной

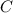. Подставим в общий интеграл начальное условие: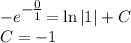
$-e^\big{- \frac{0}{1} }=\ln |1|+C\\ C=-1$

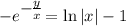$-e^\big{-\frac{y}{x} }=\ln |x|-1$ - частный интеграл, также является решением данного дифференциального уравнения.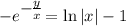

ответ: $-e^\big{-\frac{y}{x} }=\ln |x|-1$

4,8(8 оценок)

Это интересно:

Здоровье

01.02.2021

Как стать стройным естественным путем: советы от эксперта...

Компьютеры-и-электроника

10.03.2023

Как сделать снимок в Windows Live Movie Maker: подробное руководство...

Компьютеры-и-электроника

28.05.2023

Как создать ISO файл в Linux: шаг за шагом руководство...

08.02.2021