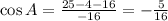; Тогда синус этого угла равен 
;
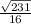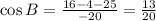; Синус этого угла: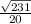
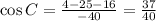; Синус этого угла:
;
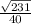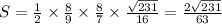
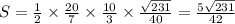
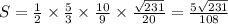
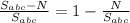- полученный результат и есть искомое соотношение. Найдем 
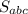: по формуле Герона получаем 
; 
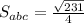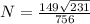; Итак, искомое отношение равно: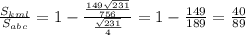 
(x-1)(x+2)не равно 0.
x-1 не равно нулю. x не равно 1.
x+2 не равно 0.x не равно -2.
x^4-5x^2+4=0
Пусть x^2=t,тогда x^4=t^2
t^2-5t+4=0
D=(-5)^2-4*1*4=9
t1=5+3/2=4
t2=5-3/2=1
Вернемся к исходной переменной.
x^2=t
x^2=4
x=плюс минус 2
x^2=1
x=плюс минус 1
y=(x-2)(x+2)(x-1)(x+1)/(x-1)(x+2)
y=(x-2)(x+1)/1
x^2+x-2x-2=0
x^2-x-2=0
X0=-(-1)/2=1/2 Y0=(1/2)^2-(1/2)-2=1/5-1/2-2=-2,5
Строим график,т.е. параболу и выкалываем точку 1 и -2.
А потом по графику смотришь где имеет одну точку,следовательно, рисуешь линию просто по y и нужно одну точку пересечения с графиком.
Вооот
Прости, что так написала
Если не понятно, то я напишу подробней
Если что я тут использовала метод "прологарифмировала два числа по одному основанию(12)"
Потом вынесла x+1 как степень по правилу
Логарифм 12 по основанию 12 равен 1