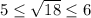
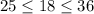
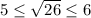 . Возведя все части неравенства в квадрат, получим
. Возведя все части неравенства в квадрат, получим 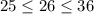 . Неравенства выполняются, следовательно, число √26 заключен между числа 5 и 6.
. Неравенства выполняются, следовательно, число √26 заключен между числа 5 и 6.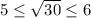 . Возведя все части неравенства в квадрат, получим:
. Возведя все части неравенства в квадрат, получим: 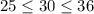 . Видим, что неравенства правильны, следовательно, число √30 заключен между числа 5 и 6.
. Видим, что неравенства правильны, следовательно, число √30 заключен между числа 5 и 6.