ответобьяснение
Объяснение:
при имеющемся знаменателе необходимо производить деление такого типа функции как
y
=
x
+
2
⋅
x
x
4
−
1
;
при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа
y
=
√
x
+
1
или
y
=
x
√
2
3
⋅
x
+
3
;
при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как
y
=
5
⋅
(
x
+
1
)
−
3
,
y
=
−
1
+
x
1
1
3
,
y
=
(
x
3
−
x
+
1
)
√
2
, которые определены не для всех чисел;
при наличии переменной под знаком логарифма или в основании вида
y
=
ln
x
2
+
x
4
или
y
=
1
+
log
x
−
1
(
x
+
1
)
причем основание является числом положительным, как и число под знаком логарифма;
при наличии переменной, находящейся под знаком тангенса и котангенса вида
y
=
x
3
+
t
g
(
2
⋅
x
+
5
)
или
y
=
c
t
g
(
3
⋅
x
3
−
1
)
, так как они существуют не для любого числа;
при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида
y
=
a
r
c
sin
(
x
+
2
)
+
2
⋅
x
2
,
y
=
a
r
c
cos
(
|
x
−
1
|
+
x
)
, область определения которых определяется ни интервале от
−
1
до
1
.при имеющемся знаменателе необходимо производить деление такого типа функции как
y
=
x
+
2
⋅
x
x
4
−
1
;
при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа
y
=
√
x
+
1
или
y
=
x
√
2
3
⋅
x
+
3
;
при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как
y
=
5
⋅
(
x
+
1
)
−
3
,
y
=
−
1
+
x
1
1
3
,
y
=
(
x
3
−
x
+
1
)
√
2
, которые определены не для всех чисел;
при наличии переменной под знаком логарифма или в основании вида
y
=
ln
x
2
+
x
4
или
y
=
1
+
log
x
−
1
(
x
+
1
)
причем основание является числом положительным, как и число под знаком логарифма;
при наличии переменной, находящейся под знаком тангенса и котангенса вида
y
=
x
3
+
t
g
(
2
⋅
x
+
5
)
или
y
=
c
t
g
(
3
⋅
x
3
−
1
)
, так как они существуют не для любого числа;
при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида
y
=
a
r
c
sin
(
x
+
2
)
+
2
⋅
x
2
,
y
=
a
r
c
cos
(
|
x
−
1
|
+
x
)
, область определения которых определяется ни интервале от
−
1
до
1
.
ответы даны в различных системах счисления.
1) Числа 55 и 13 даны в  -ичной системе счисления:
-ичной системе счисления:
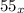 и
и 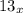
Максимальная цифра данных чисел - 5, значит, система счисления может содержать не менее 6 цифр (от 1 до 5 и 0), это означает, что оно может быть записано в шестиричной и выше системах счисления.
Получаем ОДЗ для х. => x≥6
2) Аналогично для чисел 31 и 24, которые даны в 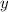 -ичной системе счисления:
-ичной системе счисления:
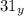 и
и 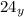
Максимальная цифра данных чисел - 4, значит, система счисления может содержать не менее 4 цифр (от 1 до 4 и 0), это означает, что оно может быть записано в пятиричной и выше системах счисления.
Получаем ОДЗ для у. => у≥5
3) Берем числа 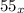 и
и 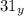 , обозначающие одну и ту же величину.
, обозначающие одну и ту же величину.
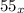 =
= 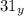
Получаем уравнение:
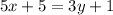
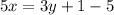
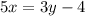
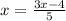
А далее методом подбора, учитывая ОДЗ x≥6 и у≥5; x;y-целые числа.
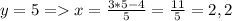 не удовлетворяет ОДЗ
не удовлетворяет ОДЗ
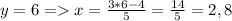 не удовлетворяет ОДЗ
не удовлетворяет ОДЗ
..............................................................................
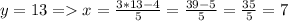
Получаем

4) 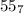 =5*7+5=40
=5*7+5=40
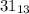 =3*13+1=40
=3*13+1=40
Всего 40 участников.
Область определения данной функции будет являться множеством значений, те
(
Аналогично для второй функции. ответ тотже
Область определения данной функции
Значит область значений будет