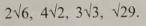
Рассмотрим выражение: (a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc =
= a² + b² + c² + 2(ab+bc+ac) = a² + b² + c² + 2*13 = a² + b² + c² + 26, то есть
(a + b + c)² = a² + b² + c² + 26. С другой стороны по условию: а+b+c=5 ⇒
5² = a² + b² + c² + 26 ⇒ 25 = a² + b² + c² + 26, значит a² + b² + c² = - 1 < 0, что невозможно, если считать числа a, b, c действительными. А значит, они таковыми не являются.
ответ: поскольку сумма квадратов трех чисел отрицательна, то таких действительных чисел a, b, c, для каких выполнены равенства в условии – не существует.
14
Объяснение:
Пусть a булочек посыпаны только корицей, b - только сахаром, c - с корицей и сахаром, d - без ничего.
Тогда:
a+b+c+d =45
a+c=12
b+c= 22
1 утверждение: d>=5
Максимум булочек с посыпкой (любой) может быть, когда c=0. Тогда d=11.
Второе с>=3, неверно, контрпример:может быть , что а=12, b=22, c=0, d=11
Третье a=b=0, можно привести контр пример распределения посыпок, как в утверждении.
Четвертое: c<13, да. Даже если все посыпанные корицей будут так же посыпаны сахаром, то таких булочек будет максимум 12.
2√6
Объяснение:
загоняем все под корень и сравниваем подкоренные числа
2√6 4√2 3√3 √29
√(4×6) √(16×2) √(9×3) √29
√24 √32 √27 √29
наименьшее 2√6