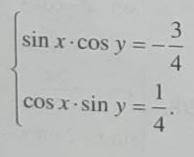
1)1/x-1=2/x+1 2)x/x-5=x-2/x-6
1/x-1=2/x+1,x≠1,x≠-1 x/x-5=x-2/x-6,x≠5,x≠6
x+1=2(x-1) x*(x-6)=(x-2)*(x-5)
x+1=2x-2 x^2-6x=x^2-5x-2x+10
x-2x=-2-1 -6x=-5x-2x+10
-x=-3 -6x=-7x+10
x=3,x≠1,x≠-1 -6x+7x=10
x=3 x=10,x≠5,x≠6
3) 3/y-2=2/y-3 x=10
3/y-2=2/y-3,y≠2,y≠3 4)z+1/z-1=z-5/z-3
3(y-3)=2(y-2) z+1/z-1=z-5/z-3,z≠1,z≠3
3y-9=2y-4 (z+1)*(z+3)=(z-5)*(z-1)
3y-2y=-4+9 z^2-3z+z-3=z^2-z-5z+5
y=-4+9 -3z+z-3=-z-5z+5
y=5,y≠2,y≠3 -2z-3=-6z+5
y=5
Объяснение:
Задание 1
\displaystyle \left \{ {{y=4-x} \atop {x^{2} +3xy=18}} \right. \\ \\
Значение у из первого уравнения подставим во второе уравнение
\displaystyle x^{2} +3x(4-x)= 18\\ \\ x^{2} +12x-3x^{2} =18\\ \\ -2x^{2} +12x-18=0 | : (-2)\\ \\ x^{2} -6x+9=0\\ \\ D= 6^{2}- 4*9= 36-36=0
Если дискриминант равен нулю , то квадратное уравнение имеет только один действительный корень, также можно сказать , что квадратное уравнение имеет два действительных корня , которые равны между собой.
x_{}= \frac{6+0}{2}= 3
y_{}= 4-3=1
Задание 2
\displaystyle \left \{ {{x^{3} - y^{3} =26} \atop {x^{2}+xy+y^{2} =13}} \right.
первое уравнение в системе это разность кубов, разложи на множители:
\displaystyle x^{3} - y^{3} = 26 \\ \\ (x-y)(x^{2} +xy+y^{2})= 26
из второго уравнения подставим значение выражения х²+ху+у²
\displaystyle 13*(x-y)= 26 \\ \\ x-y= 26 : 13\\ \\ x-y= 2 \\ \\ x= 2+y
подставим значение х во второе уравнение системы :
(2+y)^{2} +y(2+y)+y^{2} = 13\\ \\ 4+4y+y^{2} +2y+y^{2} +y^{2}= 13\\ \\ 3y^{2} +6y+4-13=0\\ \\ 3y^{2}+6y-9=0 | : 3\\ \\ y^{2}+2y-3=0\\ \\ D= 2^{2}- 4*(-3)= 4+12=16\\ \\ \sqrt{D}= 4\\ \\ y_{1}= \frac{-2+4}{2}= 1\\ \\ y_{2}= \frac{-2-4}{2} = -3
тогда
x_{1}= 2+1=3\\ \\ x_{2}= 2+(-3)= 2-3=-1
Корни уравнения ( 3 ;1) и ( -1 ; -3)
Сложим и вычтем оба уравнения и получим равносильную систему:
Сложим уравнения и найдем x
Теперь выразим y
ответ: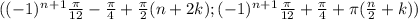 n,k ∈ Z
n,k ∈ Z