
1) a)y=3 б)x=3 в) (3;+∞) возрастает (-∞;3) убывает
2)а)у=-0,5 б) у=0,25 в) у=3
3) у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Объяснение:
1) находим по графику абсцисса -это х ордината это -у
2)подставляем вместо х значение и считаем
3) a)у(4)=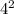 =16 б)у(-3)=
=16 б)у(-3)=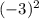 =9 в) у(2)=
=9 в) у(2)=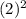 =4
=4
у(3)=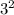 =9 у(-2)=
=9 у(-2)=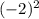 =4 у(-5)=
=4 у(-5)=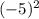 =25
=25
у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Дана точка А(-2;7), значит ее абсцисса равна -2, ее ордината равна 7
1) Ордината точки A меньше её абсциссы - Неверно, ордината точки А больше абсциссы.
2) Точка A лежит в третьей координатной четверти - Неверно, в третьей координатной четверти абсцисса и ордината отрицательны, у точки А ордината положительна.
3) Точка A находится в нижней полуплоскости - Неверно, в нижней полуплоскости ордината отрицательна, у точки А ордината положительна.
4) Точка A находится в левой полуплоскости - Верно, в левой полуплоскости абсцисса отрицательна.
5) Точка A лежит на оси ординат - Неверно, на оси ординат абсцисса равна нулю, у точки А абсцисса не равна нулю.
ответ: Точка A находится в левой полуплоскости
u=12; y=6
Объяснение:
из первого уравнения, умножить обе части на 6, получим: u+y-2*(u-y)=6 => 3y-u=6 => u=3y-6
подставим во второе, умножить его на 6: 2u-y-2*(3u+2y)=-78 => -4u-5y=-78 => 4(3y-6)+5y=78 => 17y=102 => y=6
u=3y-6 => u=3*6-6 => u=12