
Пусть х дм - длина стороны первого квадрата; (ОДЗ: x>0)
у дм - длина стороны второго квадрата, (ОДЗ: y>0)
тогда
х² дм² - площадь первого квадрата;
у² дм² - площадь второго квадрата.
По условию сумма их площадей равна 25 дм², получаем первое уравнение:
x² + y² = 25
По условию произведение длин сторон данных квадратов равно 12дм², получаем второе уравнение:
xy = 12
Решаем систему:
{x²+y² = 25
{xy = 12
Второе уравнение умножим на 2.
{x²+y² = 25
{2xy = 24
Теперь сложим:
x²+ 2xy +y² = 25+24
(x+y)² = 49
1) x+y = √49 = - 7 < 0 не удовлетворяют ОДЗ.
2) x+y = √49 = 7
Берем уравнение
x+y = 7
и второе уравнение xy = 12 и решаем систему:
{x+y=7
{xy = 12
Из первого уравнения выразим у и подставим во второе:
y=7-x
x·(7-x) = 12
7х-x²=12
x²-7x+12 = 0
D=49-4·1·12 = 49-48=1 = 1²
x₁=(7-1)/2=6/2=3
x₂=(7+1)/2=8/2=4
Найдем у:
y₁=7-3=4
y₂=7-4=3
ответ: (3дм; 4дм) или (4дм; 3дм)
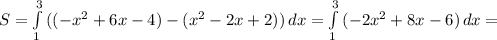
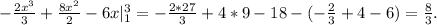
Как известно, число является кратным корнем многочлена тогда и только тогда, когда это число является корнем не только самого многочлена, но и его производной. Имеем: