Сумма смежных углов равна 180 градусам.
Зная это составим уравнение:
4x + x = 180
5x = 180
x = 36
Значит один из углов равен 36°, а другой 144°
ответ: 36° ; 144° .
.
.
.
. Но 
фактически лишнее неравенство, оно выполняется автоматически потому, что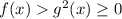 
, ибо полный квадрат всегда неотрицателен.
Чтобы сравнить числовые выражения (√6 + √10) и (3 + √7), возведем оба выражения в квадрат.
(√6 + √10)^2 = (√6)^2 + 2√6√10 + (√10)^2 = 6 + 2√60 + 10 = 16 + 4√15;
(3 + √7)^2 = 3^2 + 2 * 3√7 + (√7)^2 = 9 + 6√7 + 7 = 16 + 6√7.
В выражениях 16 + 4√15 и 16 + 6√7 первые слагаемые равны, поэтому надо сравнить вторые слагаемые. Возведем их во вторую степень.
(4√15)^2 = 16 * 15 = 240;
(6√7)^2 = 36 * 7 = 252.
240 < 252, значит 4√15 < 6√7, поэтому (16 + 4√15) < (16 + 6√7), следовательно (√6 + √10) < (3 + √7).
значит 1-ый угол=х
второй = 4х
4х+х=180°
5х=180°
х=36°
ответ: 36°; 144°
(сделайте ответ лучшим, если не трудно)