Объяснение:
у=-1/2х^2+х-1
Коэффициент перед х² отрицательный,значит ветви параболы направлены вниз. Число по модулю меньше 1. значит парабола "шире" параболы Х².Парабола имеет максимум.находим точки на оси Х.
у=0=-1/2х^2+х-1 *2
0=-х²+2х-2 ищем корни (-2±√(4-4*(-1)(-2))/(2*(-1)) =(-2±√(-4))/(-2)корней нет. Значит парабола целиком ниже оси Х.
ищем координаты вершины параболы.
Х вершины равен -в/2а=-1/(-1)=1
У вершины равен У=-1/2+1-1 =-1/2
(1;-1/2) вершина.
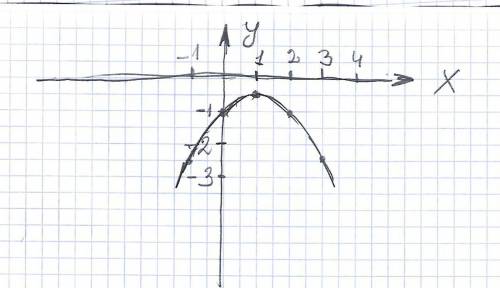
Строим таблицу х -1 0 1 2 3
у -2,5 -1 -0,5 -1 -2,5
Точка пересечения с осью У при Х=0 у= 0+0-1 =-1 (0;-1)
Тепербь наносим эти точки на оси координат и соединяем плавной кривой. Свойства. Возрастает при х∠1 ,убывает при 1∠х .
отрицательна при всех значениях Х. вершина-точка максимума.
Объяснение:
у=-1/2х^2+х-1
Коэффициент перед х² отрицательный,значит ветви параболы направлены вниз. Число по модулю меньше 1. значит парабола "шире" параболы Х².Парабола имеет максимум.
находим точки на оси Х.
у=0
0=-1/2х^2+х-1 *2
0=-х²+2х-2
ищем корни (-2±√(4-4*(-1)(-2))/(2*(-1)) =(-2±√(-4))/(-2)корней нет. Значит парабола целиком ниже оси Х.
Х вершины равен -в/2а=-1/(-1)=1
У вершины равен У=-1/2+1-1 =-1/2
(1;-1/2) вершина.
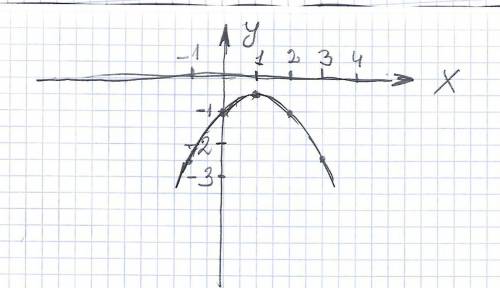
Строим таблицу х -1 0 1 2 3
у -2,5 -1 -0,5 -1 -2,5
Точка пересечения с осью У при Х=0 у= 0+0-1 =-1 (0;-1)
Наносим эти точки на оси координат и соединяем плавной кривой. Свойства. Возрастает при х∠1 ,убывает при 1∠х .
отрицательна при всех значениях Х. вершина-точка максимума.
Что ж тут хитрого: подставляем вместо Х первое число из пары, а вместо У второе и смотрим результат:
1) для пары (-6;8)
-6 +8 = 2, пока все верно,но
-18 - 16 не равно 6
значит, пара не является решением данной системы
2) для (0;-3)
0 - 3 не равно 2
т.е. и эта пара не является решением данной системы
1) для (2;0)
2 + 0 = 2, пока все верно, и
6 - 0 = 6 тоже получилось равенство!
Значит эта пара - решение системы!
Ура!))